树木造型在当今社会各行业中广泛使用，尤其在农业农事、动画视频、教学场景等行业对逼真树木模型有着较高的需求，因此，建立基于自然界中复杂外力下真实的树木模型是当今的研究热点，同时也是积极拓宽树木模型使用领域的关键[1-4].本文针对在自然环境中，建立能够模拟出风、雨等复杂外力作用下的树木动态模型为研究内容，构造真实树木摆动、断裂等姿态的动态模型算法.
国内外学术界、产业界有很多关于树木模型的研究[5-10]，如经典的分形L-system算法等，但是分形算法主要利用迭代、递归等技术来实现某一具体的分形构造.由于采用自相似性构造出的树木模型缺少真实感，与自然界中的树木有很大的差距，并且分形算法构造出的树木模型多是静态模型，难以反映出树木在自然界中遭遇风、雨等多种因素作用后的动态姿态[11-12].
本文采用在静态模型的基础上构建动态模型的方法来搭建树木整体模型[13]，主要研究断裂分支的运动轨迹以及与其他树枝、叶片的碰撞、挤压作用，建立算法以描绘其碰撞过程.
1 树木碰撞描述
自然界中的树木各分支对象，如树枝、叶片和果实等，受到外力后均有从树木主干部分断裂的可能.断裂后，叶片由于质量较小，在下落过程中对于其他对象产生的影响很小，叶片的撞击力可以忽略不计，只需考虑风、雨等外力的影响即可.而树枝和果实的质量不可忽略，所以在其运动过程中，不但要考虑外力的作用，还要考虑断裂对象的自身重力.外力的组成较为复杂，在自然环境中外力存在于整个空间且包裹作用于树木对象，对断裂对象的运动轨迹产生一定影响.本文以风力作为外力的典型代表，结合树木各分支对象的自身重力和断裂极限来建立树木动态模型[14-15].
在整个碰撞过程中，断裂下落的树枝(简称broken_branch_A)和其他树枝(简称branch_B)的形体不定，但是二者在发生碰撞时的接触点即碰撞点是一定的，因此在建模过程中，将broken_branch_A和branch_B的接触点视为球体进行讨论[16].本文以在自然界外力作用下树木各部分对象间的碰撞、挤压为研究对象建立动态模型.
2 碰撞模型算法分析
结合broken_branch_A和branch_B二者发生碰撞的实际情况，可以将断裂下落的broken_branch_A和branch_B的碰撞分为正向碰撞和侧向碰撞.二者发生碰撞时的速度与二者球心的连线在同一条直线上，且碰撞后二者的速度仍会沿着这条直线，则视为正向碰撞；二者发生碰撞时的速度与二者球心的连线不在同一条直线上，且碰撞后二者的速度都会偏离这条直线，则视为侧向碰撞.
设broken_branch_A和branch_B的质量为MbbA和MbB，半径为RbbA和RbB，杨氏模量为EbbA和EbB，泊松比为μbbA和μbB.broken_branch_A与branch_B发生碰撞后，将撞击力与branch_B的断裂极限值比较可得：撞击力高于断裂极限值时，branch_B发生断裂；反之branch_B不发生断裂，只在外力作用下进行摆动.
2.1 broken_branch_A和branch_B的正向碰撞
2.1.1 broken_branch_A垂直方向与branch_B发生正向碰撞
在发生碰撞的整个过程中，随着broken_branch_A和branch_B间的撞击面积增大以及接触时长的增加，撞击力IMPACT_F也逐渐增加到最大值，branch_B受到碰撞后的状态由IMPACT_F与branch_B的断裂极限值相比较可知，撞击力高于断裂极限值时，branch_B发生断裂；反之branch_B只有摆动，不发生断裂.二者的接触时间可以通过弹性力学公式计算得出，即
T=tcmp+trec=
(1)
式中：vpre_r_v为发生碰撞前二者的相对速度；tcmp为碰撞接触时二者相互挤压的时间；trec为二者碰撞接触后相互离开的时间；Mw_q为二者的权重质量，
为弹性恢复系数；n为与IMPACT_F相关的系数.碰撞力即撞击力IMPACT_F的特征值表达式为
(2)
式中：Dcmp为二者接触中心的挤压距离；n=
根据力学相关知识，当碰撞部分是完全弹性碰撞时，tcmp=trec，弹性恢复系数为1；当碰撞部分是完全非弹性碰撞时，tcmp+trec=∝，弹性恢复系数为0，即碰撞后对象断裂.令RbbA=∝，MbbA=∝，vpre_r_v=vpre_v，vpre_v为broken_branch_A碰撞branch_B前的速度，则接触时间为
(3)
式中：
和hpost_bbA分别为broken_branch_A落下的高度和碰撞后反弹的高度.
2.1.2 broken_branch_A水平方向与branch_B发生正向碰撞
复杂外力作用于broken_branch_A和branch_B时，当复杂外力与二者自身重力相差过大时，二者的重力可忽略不计，仅需考虑二者在复杂外力作用下在水平方向发生碰撞所构建的动态模型.二者发生碰撞时的撞击力为
2.2 broken_branch_A和branch_B的侧向碰撞
自然环境中无风、雨等外力作用或外力小于树木自身重力的条件下，broken_branch_A与branch_B发生侧向碰撞.
树木对象表面不光滑，相互发生碰撞接触时，broken_branch_A和branch_B的球体接触点存在相互压力NBA和NAB，即撞击力IMPACT_F.接触点切线方向上存在摩擦力fBA和fAB.由于二者发生侧向碰撞，树枝branch_B对broken_branch_A的NBA和fBA的合力方向也会偏离接触点连心线，互相碰撞挤压后的运动也将偏离原有的运动轨迹.
broken_branch_A在断裂后的运动过程中与branch_B发生侧向碰撞，摩擦系数为Q，vpost_v_B为branch_B被碰撞后的速度，Δtcoll为二者的碰撞时间，γ为二者球体接触点连线与碰撞后branch_B速度方向的夹角，则撞击力为IMPACT_F=NAB=
碰撞后branch_B的运动角度为δ.
2.2.1 broken_branch_A在下落过程中与branch_B发生侧向碰撞
broken_branch_A在下落途中与branch_B发生侧向碰撞，图1a为二者质量差距较小的情况，图1b为branch_B质量明显大于broken_branch_A质量的情况.
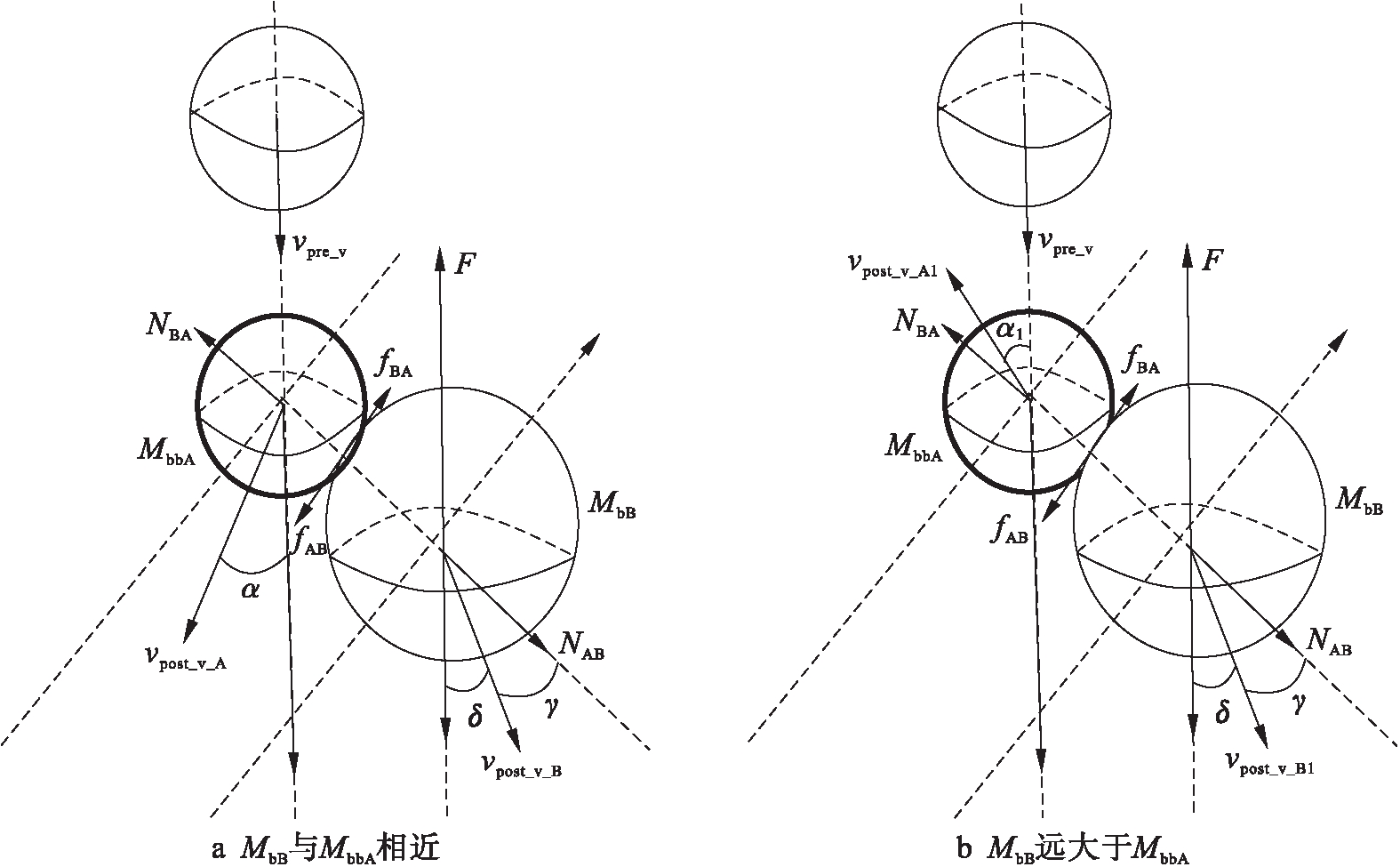
图1 下落途中无外力作用下发生侧向碰撞
Fig.1 Side collision without external force in falling process
根据图1a计算broken_branch_A和branch_B质量差距较小情况下发生侧向碰撞后的vpost_v_A、vpost_v_B和α，其表达式为
式中：
根据图1b计算branch_B质量明显大于broken_branch_A质量的条件下发生侧向碰撞后的vpost_v_A1、vpost_v_B1和α1，其表达式为
2.2.2 broken_branch_A在上升过程中与branch_B发生侧向碰撞
broken_branch_A在上升过程中与branch_B发生侧向碰撞，图2a为二者质量差距较小的情况，图2b为branch_B质量明显大于broken_branch_A质量的碰撞情况.
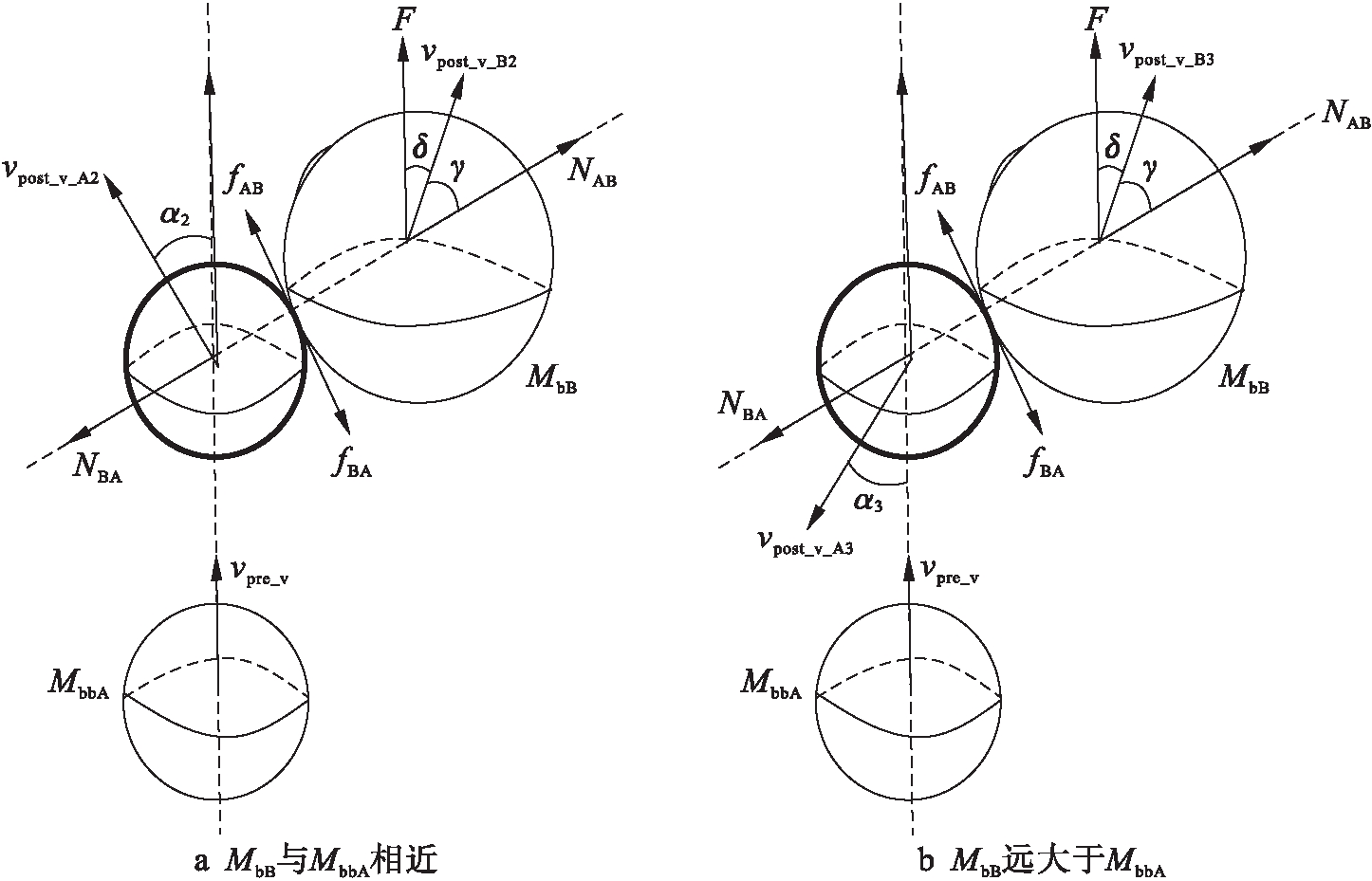
图2 上升途中无外力作用下发生侧向碰撞
Fig.2 Side collision without external force in rising process
根据图2a计算两树枝质量相差不大情况下发生侧向碰撞后的vpost_v_A2、vpost_v_B2和α2，其表达式为
式中：
根据图2b计算branch_B质量明显大于broken_branch_A质量情况下发生侧向碰撞后的vpost_v_A3、vpost_v_B3和α3，其表达式为
2.2.3 外力作用下broken_branch_A在下落过程中与branch_B发生侧向碰撞
当外力与broken_branch_A重力相差较小时，或外力不可忽略的情况下，broken_branch_A在下落过程中与branch_B发生侧向碰撞，图3a为二者质量差距较小的情况，图3b为branch_B质量明显大于broken_branch_A质量的碰撞情况.
根据图3a计算两树枝质量相差不大情况下发生侧向碰撞后的vpost_v_A4、vpost_v_B4和α4，其表达式为
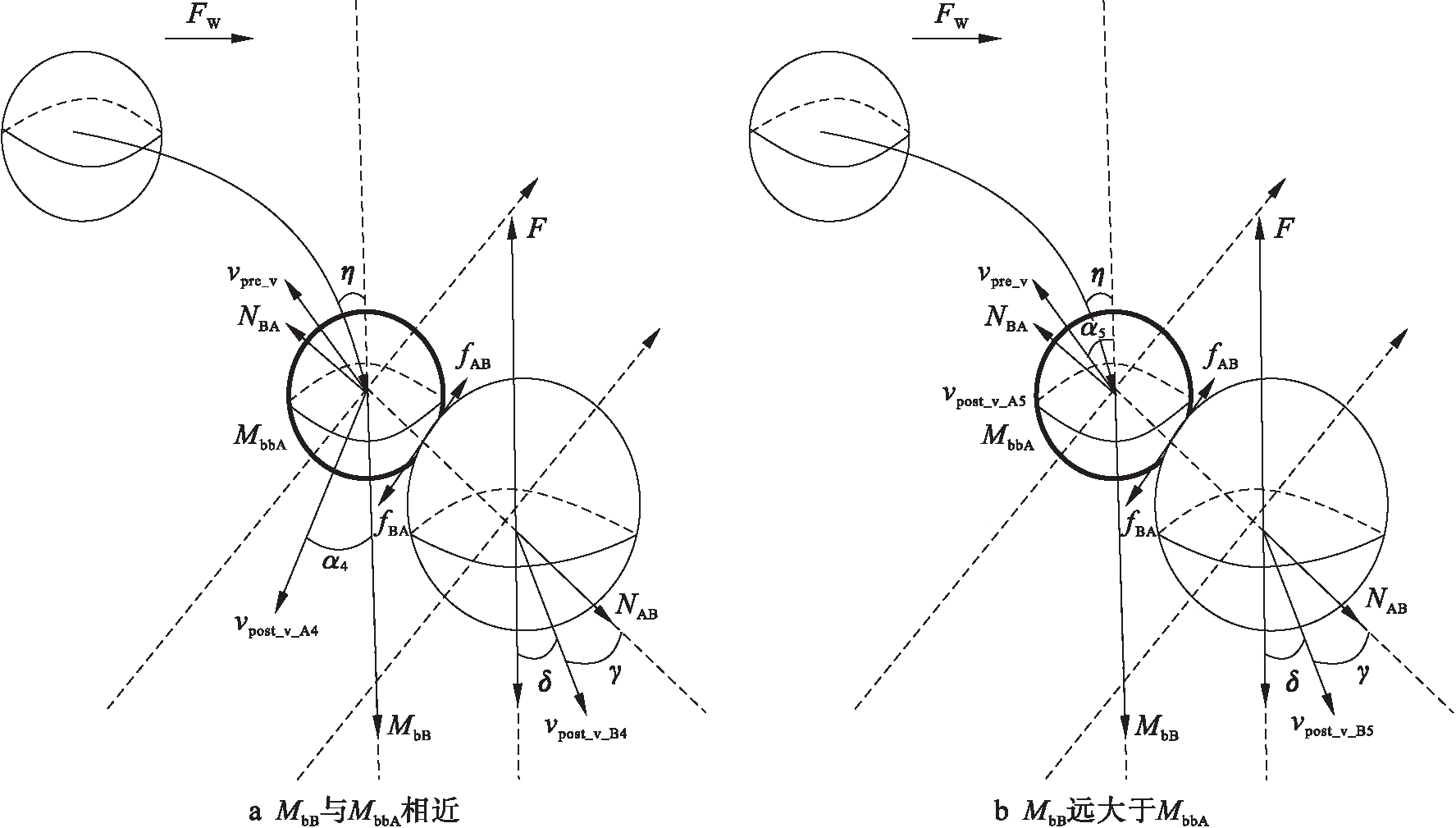
图3 下落途中外力作用下发生侧向碰撞
Fig.3 Side collision with external force in falling process
式中：
A7=cos(δ+γ-η)
A8=cos(δ+γ)
A9=A11/A10
A10=-MbBsin(δ+γ)+MbbAcsc δcos γ+
MbBcos(δ+γ)csc δcos δ
A11=-MbBvpre_vA7+MbBA8vpre_vsin ηcsc δcos δ-MbBA8·
vpre_vcos η+MbbAvpre_vsin ηcsc δcos γ-MbBA8gΔtcoll
根据图3b计算branch_B质量明显大于broken_branch_A质量情况下发生侧向碰撞后的vpost_v_A5、vpost_v_B5和α5，其表达式为
式中，
A12=-A11/A14
2.2.4 外力作用下broken_branch_A在上升过程中与branch_B发生侧向碰撞
当外力与broken_branch_A重力相差较小时，或外力不可忽略的情况下，broken_branch_A在上升过程中与branch_B发生侧向碰撞，图4a为二者质量差距较小的情况，图4b为branch_B质量明显大于broken_branch_A质量的碰撞情况.
根据图4a计算两树枝质量相差不大情况下发生侧向碰撞后的vpost_v_A6、vpost_v_B6和α6，其表达式为
式中：
A13=A15/A14
A14=MbBsin(δ+γ)+MbbAcsc δcos γ+
MbBcos(δ+γ)csc δcos δ
A15=MbBvpre_vA7-MbBA8vpre_vsin ηcsc δcos δ+
MbBA8vpre_vcos η-MbbAvpre_vsin ηcsc δcos γ-
MbBA8gΔtcoll
根据图4b计算branch_B质量明显大于broken_branch_A质量的情况下发生侧向碰撞后的vpost_v_A7、vpost_v_B7和α7，其表达式为
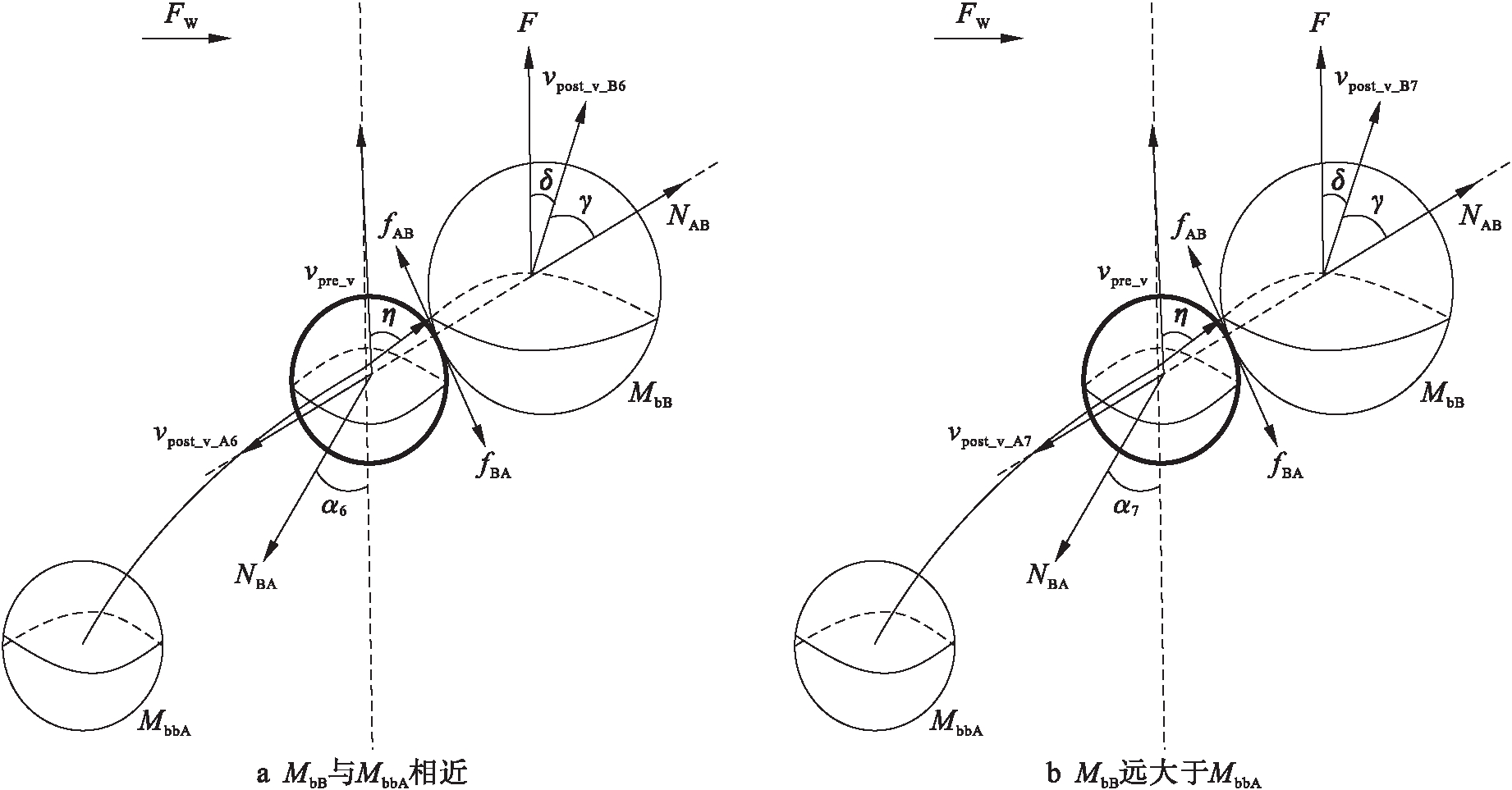
图4 上升途中外力作用下发生侧向碰撞
Fig.4 Side collision with external force in rising process
2.2.5 外力作用下broken_branch_A在水平方向上与branch_B发生侧向碰撞
在自然界中，风等外力作用于broken_branch_A、branch_B时，外力远远大于二者自身重力时，broken_branch_A在外力作用下沿着外力方向做加速运动，示意图如图5所示.
根据图5计算两树枝发生侧向碰撞后的vpost_v_A8、vpost_v_B8和α8，其表达式为
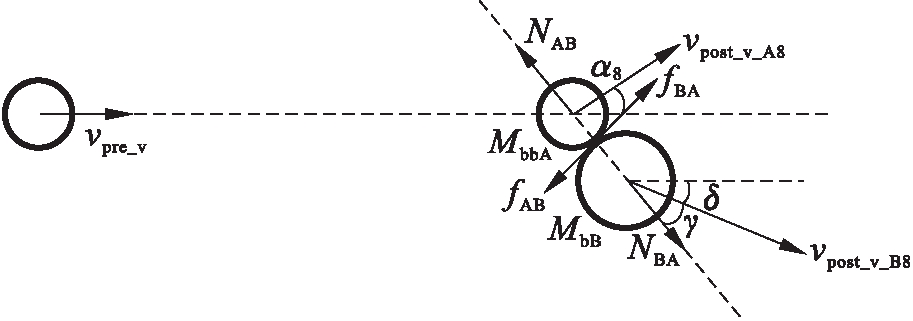
图5 broken_branch_A和branch_B发生侧向碰撞
Fig.5 Side collision of broken_branch_A with branch_B
α8=arcsin(A16A17)
式中：
2.3 抛物线模型
2.3.1 broken_branch_A碰撞后的上升轨迹模型
broken_branch_A与branch_B在D(xD，yD)点发生碰撞后，broken_branch_A反向运动，反弹到E点后，在外力和自身重力作用下落地F点，示意图如图6所示.
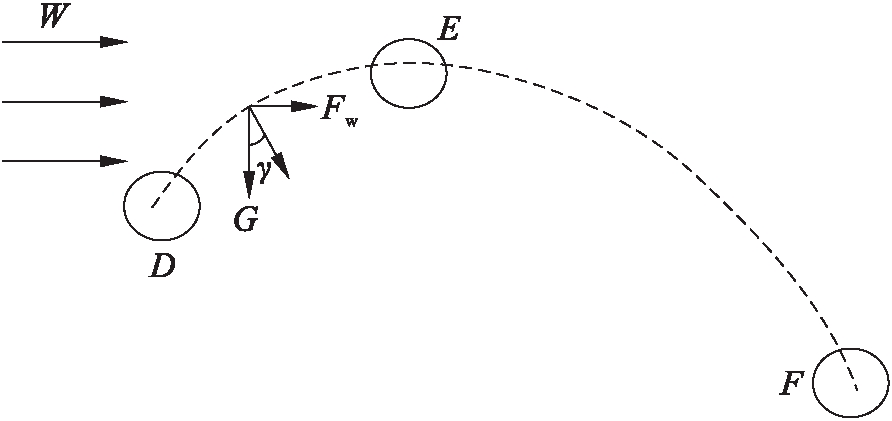
图6 运动轨迹示意图
Fig.6 Schematic diagram of trajectory
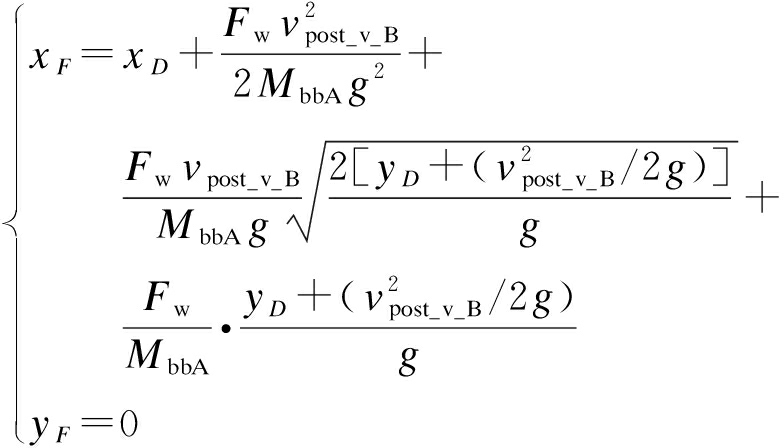
由于初始速度为
可以得到实际上升高度E点坐标和F点坐标为
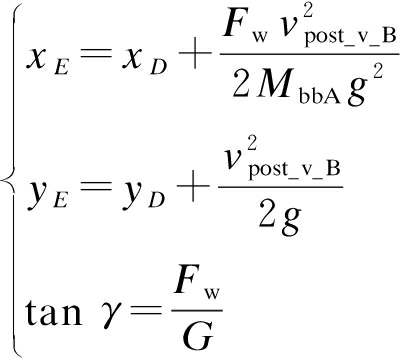
2.3.2 broken_branch_A碰撞后运动过程中没有接触其他对象
broken_branch_A在自然界中断裂后没有接触其他对象，broken_branch_A做抛物线运动直至落地，示意图如图7所示.
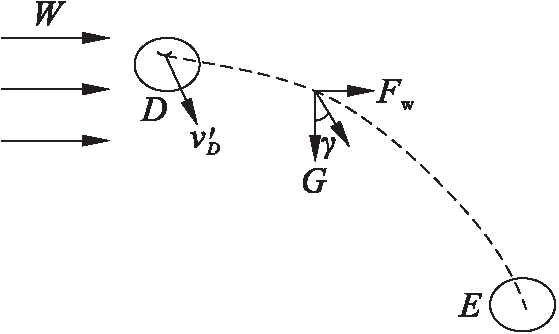
图7 下落轨迹示意图
Fig.7 Schematic diagram of falling trajectory
由D点(xD，yD)中的纵坐标yD=v′Dcos γtDE+
可求出时间
从而求出E点坐标为
3 实验模拟
图8为运动学模型成像图.随着风力的逐渐增大，树枝逐渐倾斜，摆动幅度加大，最终发生断裂.图8a为1级风力情况下树木的形态，枝干、叶片等无很大影响，树木各部分对象呈现静止状态；图8b为3级风力等级情况，可以看出当前风力等级对于细小的树枝对象影响较大，部分枝叶对象开始呈现摆动的姿态；图8c为4级风力等级情况，可以看出细小的树木各分支对象围绕着与上级枝干的连接处进行摆动，且摆动角度逐渐增大；图8d为风力达到6级的情况，末级的树枝、叶片等在风力作用下断裂.通过基于运动学模型模拟出的效果，可以得到逼真的树木运动姿态，模拟效果较为真实.
图8 运动学模型成像图
Fig.8 Imaging by kinematic model
4 结 论
基于自然界中存在的复杂外力与重力间的关系、树木分支对象间的碰撞角度，根据碰撞力学中的特征量获得撞击力及遭受碰撞后的树木各分支对象的运动速度及角度等数据，建立树木动态模型.采用该模型可以描绘各分支对象在断裂后运动轨迹中接触其他树枝、叶片对象后而产生新的运动轨迹及挤压、摆动等形态.经过实验模拟，基于运动学构建的树木动态模型具有复杂度低、系统反应迅速、效果真实等优点.
[1] 崔沿沾，陈宇拓，郭怡旭.人工林地形与树木融合的高效建模 [J].中南林业科技大学学报，2019，39(11)：48-55.
(CUI Yan-zhan，CHEN Yu-tuo，GUO Yi-xu.Efficient modeling for man-made forest terrain and trees integration [J].Journal of Central South University of Forestry & Technology，2019，39(11)：48-55.)
[2] 周向戈，唐丽玉，彭先敏，等.三维园林植被景观构建与虚拟展示 [J].计算机工程与应用，2019，55(7)：234-240.
(ZHOU Xiang-ge，TANG Li-yu，PENG Xian-min，et al.Three-dimensional modeling and virtual exhibition for garden landscaping [J].Computer Engineering and Applications，2019，55(7)：234-240.)
[3] 曹伟，陈动，史玉峰，等.激光雷达点云树木建模研究进展与展望 [J].武汉大学学报·信息科学版，2021，46(2)：203-220.
(CAO Wei，CHEN Dong，SHI Yu-feng，et al.Progress and prospect of LiDAR point clouds to 3D tree models [J].Geomatics and Information Science of Wuhan University，2021，46(2)：203-220.)
[4] 王雨桐.创意三维树木建模与动画技术 [D].杭州：浙江大学，2018.
(WANG Yu-tong.Creative modeling and animation of 3D trees [D].Hangzhou：Zhejiang University，2018.)
[5] 范曾.基于树木生长发育模型的自动建模算法 [D].成都：四川大学，2021.
(FAN Zeng.An automatic modeling algorithm based on tree growth and development model [D].Chengdu：Sichuan University，2021.)
[6] 杨海泉.基于空间资源竞争的树木模拟算法研究 [D].深圳：深圳大学，2019.
(YANG Hai-quan.Research on tree simulation based on competition over space resources [D].Shenzhen：Shenzhen University，2019.)
[7] 梁爽，朱作腾，贾金原.基于树型空间的三维树木模型匹配 [J].系统仿真学报，2020，32(4)：582-590.
(LIANG Shuang，ZHU Zuo-teng，JIA Jin-yuan.3D tree model matching based on tree shape space [J].Journal of System Simulation，2020，32(4)：582-590.)
[8] Li R H，Bu G C，Wang P.An automatic tree skeleton extracting method based on point cloud of terrestrial laser scanner [J].International Journal of Optics，2017，2017：1-12.
[9] 杨垠晖，王锐.树木的真实感建模与绘制综述 [J].计算机辅助设计与图形学学报，2018，30(2)：191-216.
(YANG Yin-hui，WANG Rui.Realistic modeling and rendering of trees：a survey [J].Journal of Computer-Aided Design & Computer Graphics，2018，30(2)：191-216.)
[10] 刘静霞.植物景观三维图像边缘锐化方法 [J].沈阳工业大学学报，2020，42(3)：298-302.
(LIU Jing-xia.Edge sharpening method for 3D image of plant landscape [J].Journal of Shenyang University of Technology，2020，42(3)：298-302.)
[11] Prusinkiewicz P，Lindenmayer A.The algorithmic beauty of plants [M].New York：Springer New York，1990.
[12] de Reffye P，Edelin C，Françon J，et al.Plant models faithful to botanical structure and development [J].ACM SIGGRAPH Computer Graphics，1988，22(4)：151-158.
[13] 于舜.自然环境模拟
树木建模方法研究 [D].沈阳：东北大学，2014.
(YU Shun.Natural environment simulation-research on tree modeling method [D].Shenyang：Northeastern University，2014.)
[14] 李正农，余世斌，吴红华，等.强风作用下树木周围流场的数值模拟研究 [J].中南大学学报(自然科学版)，2021，52(11)：3970-3980.
(LI Zheng-nong，YU Shi-bin，WU Hong-hua，et al.Numerical simulation of flow field around the tree in strong wind [J].Journal of Central South University (Science and Technology)，2021，52(11)：3970-3980.)
[15] Manickathan L，Defraeye T，Allegrini J，et al.Compara-tive study of flow field and drag coefficient of model and small natural trees in a wind tunnel [J].Urban Forestry & Urban Greening，2018，35：230-239.
[16] 刘茜，程靖，梁建勋.混合碰撞建模方法及其试验验证 [J].机械工程学报，2022，58(1)：116-123.
(LIU Qian，CHENG Jing，LIANG Jian-xun.Novel hybrid method for contact analysis and experiment test [J].Journal of Mechanical Engineering，2022，58(1)：116-123.)