现如今,采用爆破开挖的矿山法仍然是隧道修建的主要方法,此种方法轻则是噪声扰民,重则对地表的房屋建筑造成震动甚至产生实质性的破坏.截至2018年底,我国共建设有交通隧道36 103 km.其中,铁路隧道15 177座,长度16 331 km;公路隧道16 500座,长度15 940 km;城市轨道交通隧道5 766 km,其中地铁约4 511 km[1].随着隧道建设总长的不断增加,其爆破开挖对地面建筑物造成的负面影响已经得到了工程界和学术界的重视,科研人员通过现场爆破试验[2]、实时监测[3]、数值模拟[4]等方法和技术手段进行了广泛研究,取得了一些研究成果.
当炸药在岩石、土壤和其他介质中爆炸时,必须将一部分能量转换为地震波,并且从爆炸源迅速传播到周围的介质中,从而导致表面和建(构)筑物的振动,在一定范围内对非爆破目标的建(构)筑物造成不同程度的破坏.隧道爆破开挖影响区振动激励下地震波的传播规律和地震动速度的衰减规律是当前研究的重点.
杨云凌[5]依托长沙市地铁二号线的一段隧道,结合爆破监测数据和有限元分析模拟,阐述了隧道埋深与振速放大系数之间的关系;邹新宽等[6]通过从不同角度对大量的深孔爆破地震动测试数据的分析,得到了岩石中爆破地震波传播的频率、幅值和持续时间等主要参数的变化规律以及它们的影响因素;王蕊等[7]以某公路隧道工程掘进开挖爆破的震动安全监测项目为依托,运用数值三维模型实体建模研究隧道下穿村庄时当地民用建筑基础、圈梁、楼板、柱等不同的速度响应时程,分析得出响应规律.还有一些学者就隧道爆破开挖对其邻近隧道的影响做了分析研究[8-10].
本文在前人研究的基础上,依托爱民山隧道,利用ANSYS有限元分析软件建立三维隧道模型,经过瞬时爆破分析后,得到距离掌子面不同位置的地表震速波形图,总结地表的震动规律,判断地面建筑物的安全性,给出了爆破空洞放大效应影响区域的地表震动速度传播和衰减规律.本研究为类似工程中小净距单行线隧道爆破施工对先行隧道影响提供了科学依据与技术指导,也为类似隧道工程的爆破掘进在理论上和施工方法上提供参考借鉴.
1 工程概况
爱民山隧道位于丹东市郊附近,属于丹东市四号干线(花园路至宝山大街段),呈北东走向展布,设计为两条小净距单行线曲线隧道,属短隧道;隧道左线全长500 m,右线全长42 m,采用暗挖钻爆法施工.隧道区地表覆盖层较厚,大部分都被残积土、全风化变粒岩等所覆盖,露头较少,变粒岩节理裂隙以风化、构造裂隙为主.隧道入口段及出口段为Ⅴ2、Ⅴ1级围岩,洞身段为Ⅳ3、Ⅳ2级围岩.爱民山顶距隧道约50 m,且有民用建筑;隧道宝山大街段左线线位左侧约60 m处为元宝区抗美援朝烈士陵园,这就要求隧道的爆破施工不能对山顶的民用建筑和烈士陵园产生影响.
2 模型建立
2.1 单元类型选取
本文利用ANSYS软件的LS-DYNA模块建立实体三维模型并进行运算.由于隧道爆破是一个瞬时的动态过程,并且需要输出节点的速度波形图,所以围岩采用三维实体单元(solid164);初期支护采用壳单元(shell163),此单元有大变形、大应变能力;锚杆采用三维杆单元(link8),因为其可承受单轴的压力或拉力,符合锚杆在初支的受力特征.隧道不同层岩体的物理力学参数如表1所示.
表1 隧道岩土体物理力学参数
Tab.1 Physical and mechanical parameters of tunnel rock and soil
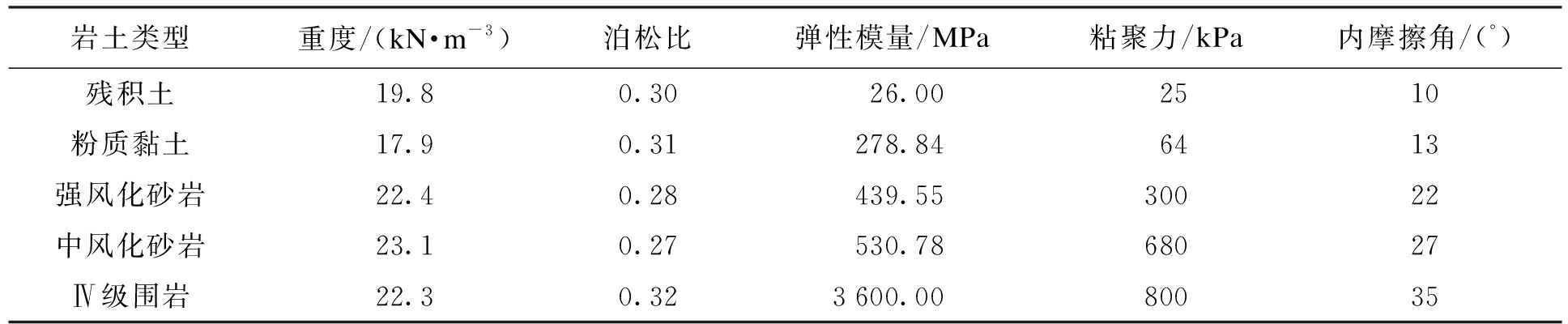
岩土类型重度/(kN·m-3)泊松比弹性模量/MPa粘聚力/kPa内摩擦角/(°)残积土19.80.30 26.002510粉质黏土17.90.31278.846413强风化砂岩22.40.28439.5530022中风化砂岩23.10.27530.7868027Ⅳ级围岩22.30.323600.0080035
2.2 边界选取
由于隧道的爆破开挖会对周围岩体及地表产生一定的影响,实践和理论分析表明,对于地下洞室开挖后的应力应变,仅在洞室周围距洞室中心点3~5倍隧道开挖宽度(或高度)的范围内存在实际影响.在3倍宽度处的应力变化一般在10%以下,在5倍宽度处一般在5%以下[11].因此,计算边界可确定在3~5倍的宽度.为减小边界效应的影响,选取长度方向为150 m,高度为100 m,隧道顶部距地表45 m,隧道距左侧隧洞为40 m,纵向深取107.5 m,其中包括前部已开挖的50 m,中部5个1.5 m正在开挖的小段以及后部未开挖的50 m.
2.3 约束施加
数值模拟采用位移边界条件,将模型的4个侧面和底部均设为无反射的固定边界,固定边界位移满足ux=uy=uz=0;地表及隧道已开挖区周边设为自由边界.
2.4 求 解
静力分析时,计算收敛准则为不平衡力比率满足10-5的求解要求,动力计算时的计算时间主要依据动力荷载时间来确定.划分完网格的模型如图1所示.
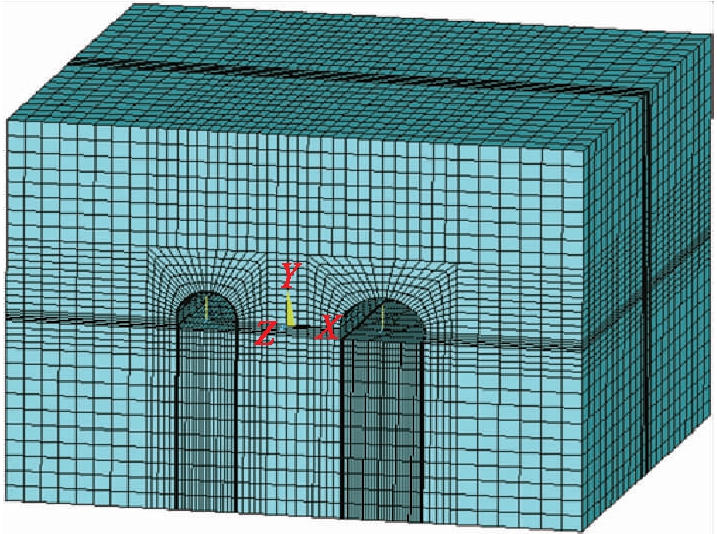
图1 隧道模型图
Fig.1 Tunnel model diagram
3 爆破荷载及时间的确定
采用ANSYS分析爆破震动的一项重要工作就是建立一个合理的爆破加载模型,这就需要确定爆破激振力的大小、方向、作用位置、峰值时刻以及持续时间等内容.查阅相关文献可知,岩体内的爆破波多以三角形荷载为主,即压力经过一个上升段到达峰值后急剧衰减.根据工程资料,爆破压力峰值取15 MPa,荷载以压力形式均布荷载作用在隧道壁和掌子面上,加载时间为12 ms,卸载时间为78 ms,取计算时间为1 s.爆破荷载时刻图如图2所示.
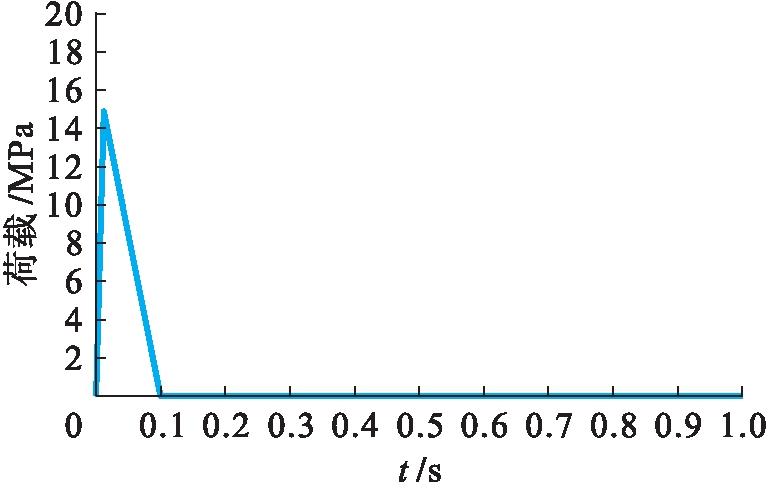
图2 爆破荷载时刻图
Fig.2 Blasting load time diagram
4 计算结果与分析
在介质中传播的扰动称为波,炸药在岩体等介质中爆炸所激起的应力扰动的传播称为爆炸应力波.大多数岩石中激起的爆炸应力波在距离爆炸点不同距离处表现为冲击波、爆炸应力波和地震波.通过分析爆炸应力波在地表产生的震速波形图,掌握其震动规律,可以对地面的建筑物及时采取合理的保护措施,或者及时调整爆破施工方案.
4.1 地表震速波形分析
本文取爆源正上方地表的44 569号节点,已开挖段距爆源15 m处地表的27 380号节点以及未开挖段距爆源15 m处地表的76 614号节点,通过施加爆破荷载后,对其震动速度进行分析,输出各节点在此1 s爆破过程的震速波形图.各个节点的震速波形图如图3~8所示.
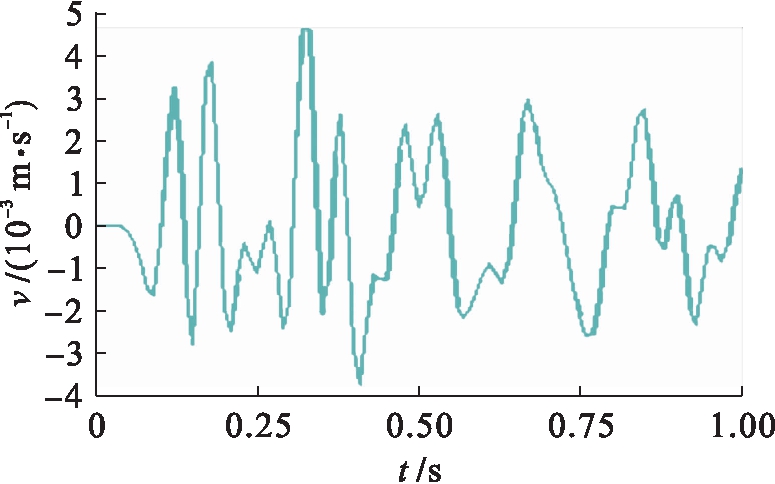
图3 爆源后方15 m处地表X方向v-t图
Fig.3 X-direction v-t diagram of ground surface at 15 m behind blasting point
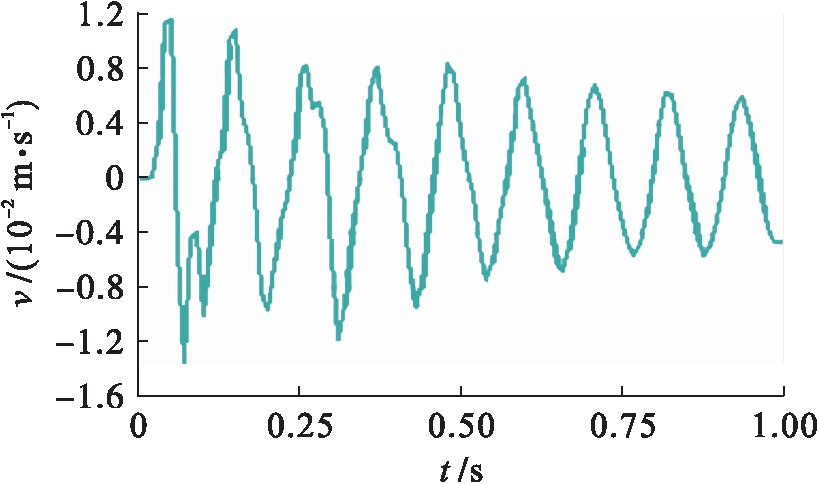
图4 爆源后方15 m处地表Y方向v-t图
Fig.4 Y-direction v-t diagram of ground surface at 15 m behind blasting point
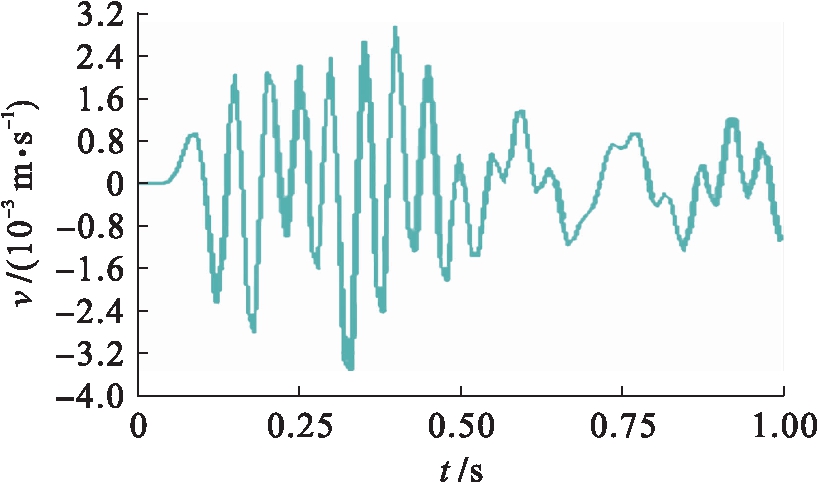
图5 爆源上方地表X方向v-t图
Fig.5 X-direction v-t diagram of ground surface above blasting point
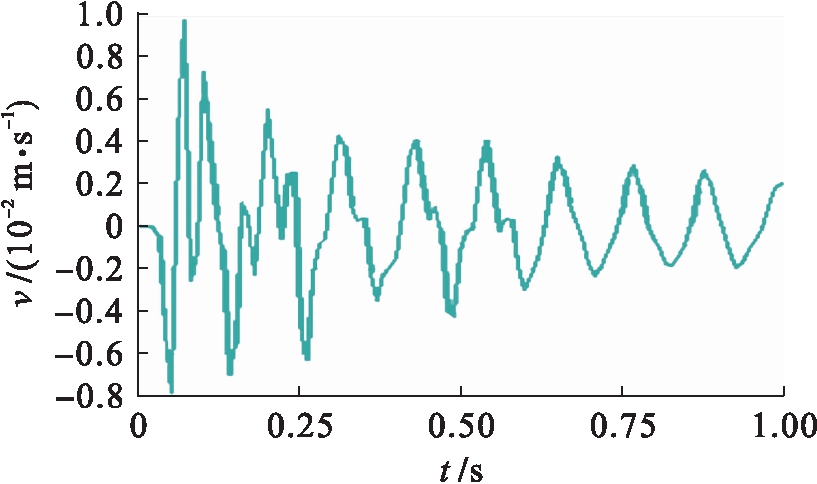
图6 爆源上方地表Y方向v-t图
Fig.6 Y-direction v-t diagram of ground surface above blasting point
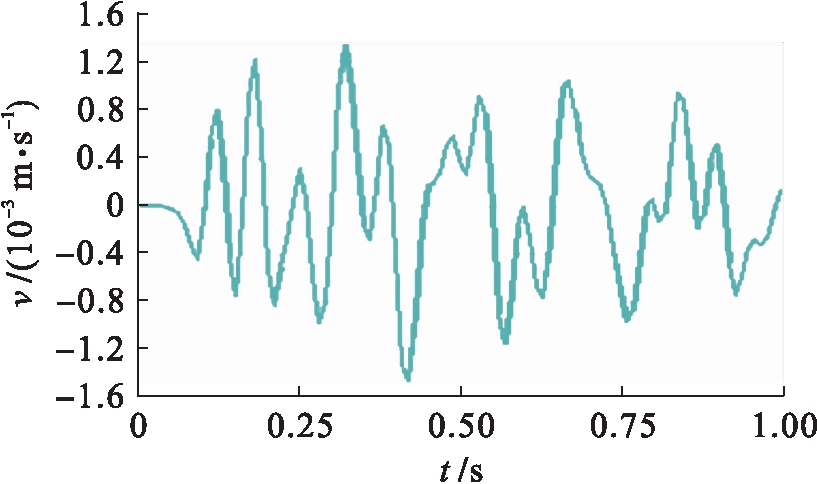
图7 爆源前方15 m处地表X方向v-t图
Fig.7 X-direction v-t diagram of ground surface at 15 m ahead of blasting point
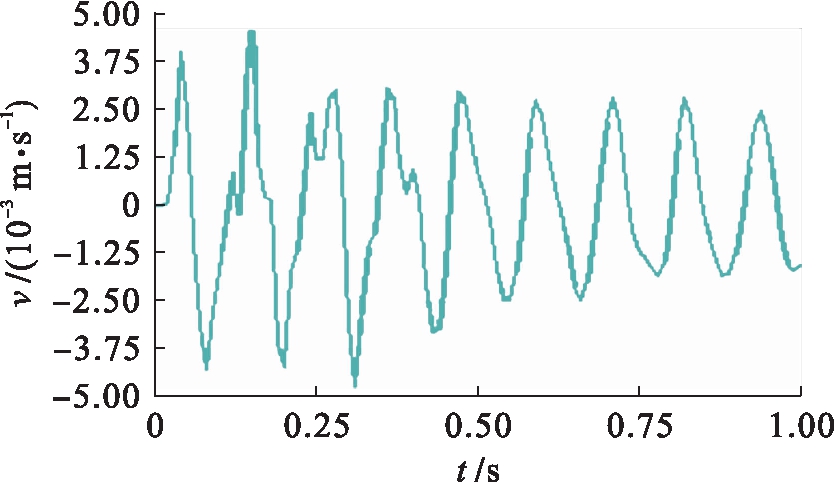
图8 爆源前方15 m处地表Y方向v-t图
Fig.8 Y-direction v-t diagram of ground surface at 15 m ahead of blasting point
爆破地震波有纵波(P波)和横波(S波)之分,纵波传播速度快,振幅小.从以上震速时程波形图可以看出,对于爆源正上方及其后15 m和前15 m处地表节点来说,X方向震速较大的部分主要集中在0.2~0.4 s之间,最大震速为爆源后方15 m处地表且数值为0.48 cm/s,0.4 s后速度峰值逐渐衰减,但相邻的波峰和波谷之间有小幅的波动.由于纵波在固体介质中的传播速度快于横波的传播速度,因此,X方向的震速峰值出现滞后性,滞后约100 ms.Y方向的震动速度较大时刻出现在0~0.2 s,0.2 s后震速逐步衰减,且衰减波形较X方向更为“规则”,即几乎未出现波峰和波谷之间的小幅波动,最大震速为爆源后方15 m处地表且数值为1.3 cm/s.
4.2 数据对比分析
占城[12]依托重庆市某隧道工程分析了城市隧道爆破对邻近建筑物的影响,该隧道采用微差光面爆破上下台阶法开挖,炮孔布置图如图9所示.
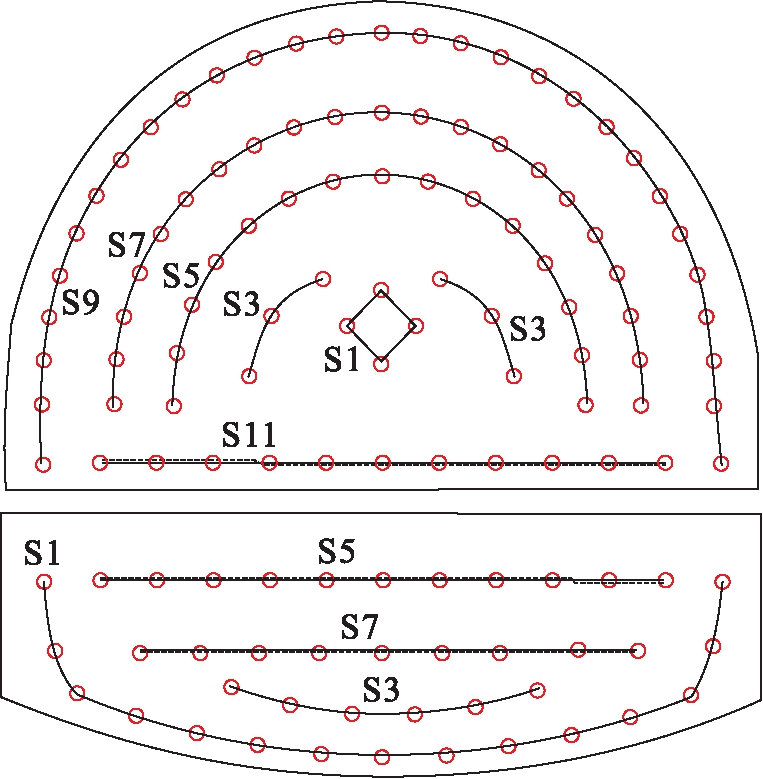
图9 炮孔布置平面图
Fig.9 Layout plane diagram of blasting holes
本工程监测采用中科测绘TC4850型爆破震动测试仪、TCS-B3三轴向振动速度传感器,测得掌子面上方X方向和Y方向的一次爆破测试典型振动时程曲线如图10所示.
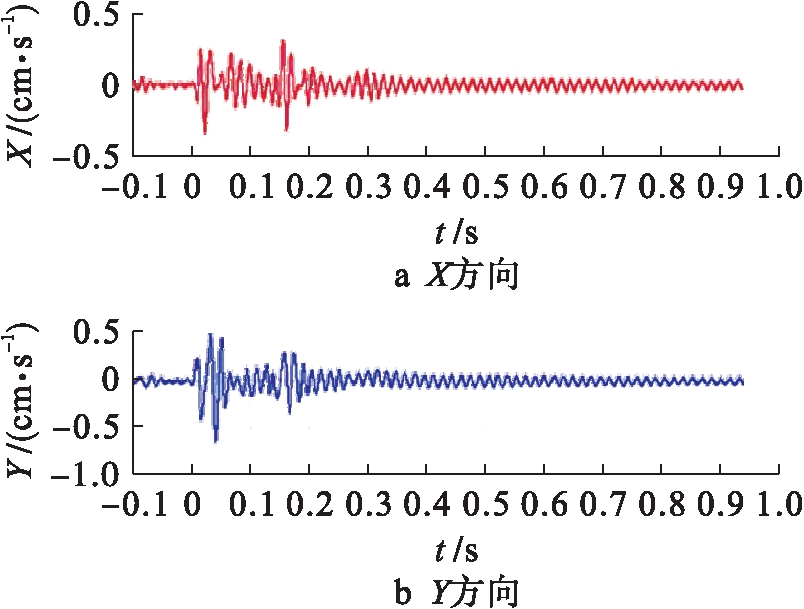
图10 测点速度的时程曲线
Fig.10 Time history curve of measuring point velocity
由图10可知,X方向的震速峰值有一定时段的滞后性,且峰值小于Y方向的峰值.这与本文模拟结果类似,说明本文模型具有一定的科学性和可信度.
4.3 地表震速衰减规律
4.3.1 爆破震动速度经验公式
根据《爆破安全规程》(GB6722-2014),测点震速与测点距爆破区域距离和炸药使用量有关,同时与爆破区域地形地质、爆破方法等因素亦有明显关系,可按萨道夫斯基经验公式进行计算,即
(1)
式中:v为爆破地震波质点的震动速度;K、α为与爆破点至测点之间的地形、地质条件有关的系数和衰减指数,应通过现场试验确定,如表2所示;Q为炸药量,齐发爆破为总药量,延时爆破为最大单段药量;R为爆破中心到测点之间的距离.
表2 爆区不同岩性的K、α值
Tab.2 K and α values of different lithologies in blasting zone
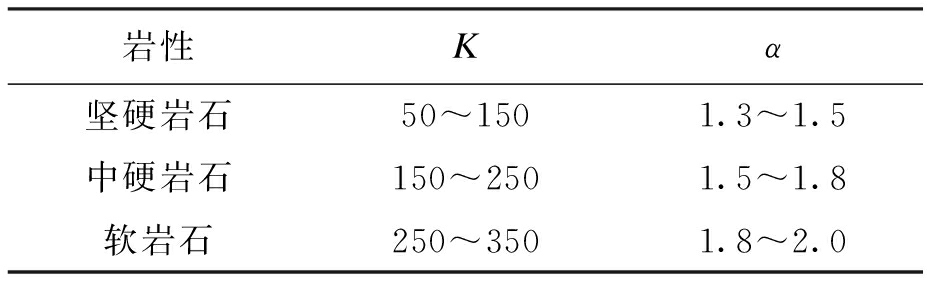
岩性Kα坚硬岩石50~1501.3~1.5中硬岩石150~2501.5~1.8软岩石250~3501.8~2.0
4.3.2 地表节点震速分析
隧道爆破时,已开挖区域的地表震动速度不能完全利用萨道夫斯基经验公式计算,且隧道已开挖区域的地表震动速度比未开挖区的震动速度要大,形成爆破空洞放大效应.对于隧道爆破空洞放大效应,一些研究人员只是对隧道掌子面前后的地表震动速度建立二维模型进行对比研究[13-15],并未详细给出爆破空洞放大效应影响区域的地表震动速度传播和衰减规律,也未对已开挖区和未开挖区地表质点的震动速度进行预测,并且预测模型较为简单,不能较好反应实际隧道工程地质情况.因此,分析地铁隧道爆破开挖过程中已开挖区和未开挖区地表震动的传播衰减规律,预测地表最大震速点的位置,确定隧道爆破开挖施工安全判据和安全距离很有必要.
以爆源(掌子面)为中心,在地表沿隧道开挖掘进方向取17个节点,相邻节点之间的距离为15 m,其中,爆源正上方的为9号节点,1~8号节点位于隧道已开挖段正上方的地表,10~17号节点位于隧道未开挖段正上方的地表,如图11所示.
图11 取点位置平面示意图
Fig.11 Schematic plane of access positions
取各节点在爆破过程中的三个方向最大震速峰值绘制曲线,如图12所示.由图12可知,在隧道开挖掘进方向取的节点中,处于已开挖段(1~8号)和未开挖段(10~17号)的节点震速峰值衰减呈现完全不同的规律.对于未开挖段,节点震速峰值随着与爆源距离的增大而逐渐减小,且衰减的速率较为缓慢,符合《规程》给出的经验公式.对于已开挖段,节点震速峰值随着与爆源距离的增大而先增大后减小,且在距离爆源25~30 m处震速峰值衰减较快,因此,不符合《规程》给出的经验公式.震速峰值的最大值并非出现在爆源正上方的地表位置,而是在已开挖区距离爆源约10 m的位置,最大值为3.23 cm/s.隧道在爆破开挖施工中,地表质点震动速度存在空洞放大效应.隧道掘进爆破震动空洞效应是指已开挖区形成的空洞导致其上部地表震动速度大于未开挖部分的地表震动速度的现象.空洞效应导致地表震动速度存在区域性变化的特点,使得处于隧道已开挖区的地表震动速度大于未开挖区地表震动速度,且二者的爆破地震波衰减规律亦不一致.
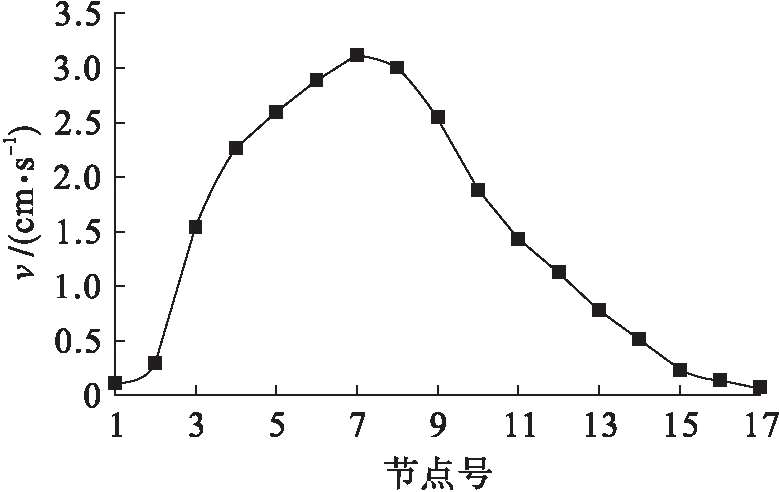
图12 地表节点震速峰值
Fig.12 Peak vibration velocity of ground surface nodes
5 结 论
本文利用ANSYS有限元分析软件对丹东市爱民山隧道进行爆破掘进开挖数值模拟,通过对一些地表特殊节点的震速波形分析,得出以下结论:
1) 根据我国现行国家标准《爆破安全规程》(GB6722-2014)规定:建(构)筑物的爆破地震震动速度应小于50 mm/s.在隧道掘进方向选取的地表16个节点中,最大的震速峰值为32.3 mm/s,这个数值小于规定的50 mm/s,所以山顶的民用建筑是安全的.
2) 在隧道爆破掘进过程中,由于纵波在固体介质中的传播速度快于横波,所以地表同一个节点不同方向大道震速峰值的时刻不同,横波有明显的滞后性.爆破地震波的震速在到达峰值后逐渐衰减,但横波会有小幅波动.
3) 由于空洞效应的存在,导致处于隧道已开挖区的地表震动速度大于未开挖区的地表震动速度,在距离爆源15~30 m处空洞放大效应最为明显.因此,在隧道爆破开挖的过程中,应该控制炸药用量,采用合理的爆破施工方案,做好已开挖隧道的支护和衬砌工作,同时对地表的一些民用建筑采取一定保护措施.
[1] 严金秀.中国隧道工程技术发展40年 [J].隧道建设,2019,39(4):537-544.
(YAN Jin-xiu.Achievements and challenges of tunneling technology in China over past 40 years [J].Tunnel Construction,2019,39(4):537-544.)
[2] 高照帅,王德胜,尹作明,等.城市地铁浅埋隧道掘进爆破地表振动试验研究 [J].山东科技大学学报(自然科学版),2016,35(1):79-85.
(GAO Zhao-shuai,WANG De-sheng,YIN Zuo-ming,et al.Experimental study of ground vibration induced by shallow urban subway tunnel excavation blasting [J].Journal of Shandong University of Science and Technology (Natural Science),2016,35(1):79-85.)
[3] 姜楠,邹锐,渠银录,等.爆破开挖附近地铁隧道振动监测数值分析 [J].工程爆破,2013,19(4):46-49.
(JIANG Nan,ZOU Rui,QU Yin-lu,et al.Numerical analysis of the subway tunnel vibration monitoring near the blasting excavation [J].Engineering Blasting,2013,19(4):46-49.)
[4] 蔡军,何忠明,林志元,等.隧道爆破开挖震动效应的数值模拟 [J].矿冶工程,2015,35(4):5-8.
(CAI Jun,HE Zhong-ming,LIN Zhi-yuan,et al.Numerical simulation of blasting vibration effect for tunnel excavation [J].Mining and Metallurgical Engineering,2015,35(4):5-8.)
[5] 杨云凌.浅埋隧道爆破振动空洞效应研究 [J].爆破,2012,29(3):127-130.
(YANG Yun-ling.Hollow effect induce by blasting vibration in shallow tunnels [J].Blasting,2012,29(3):127-130.)
[6] 邹新宽,张继春,潘强,等.浅埋小净距隧道掘进爆破引起的地表振动特性模拟分析 [J].防灾减灾工程学报,2016,36(4):646-651.
(ZOU Xin-kuan,ZHANG Ji-chun,PAN Qiang,et al.Ground vibration analysis of shallow-buried and small-interval tunnel resulting from blasting by numerical simulation [J].Journal of Disaster Prevention and Mitigation Engineering,2016,36(4):646-651.)
[7] 王蕊,宋宏伟,樊人竞.隧道下穿村庄对地面建筑爆破震动影响的研究 [J].建筑技术,2017,48(12):1290-1292.
(WANG Rui,SONG Hong-wei,FAN Ren-jing.Stu-dies on influence law of tunnel blasting vibration on ground building [J].Architecture Technology,2017,48(12):1290-1292.)
[8] 贾亮.浅埋偏压小间距隧道爆破对既有隧道震动影响分析 [J].铁道勘察,2016,42(3):36-39.
(JIA Liang.Shallow buried side small spacing tunnel blasting impact on the existing tunnel vibration analysis [J].Railway Investigation and Surveying,2016,42(3):36-39.)
[9] 孙宝平,高文学,周世生.隧道掘进爆破破岩数值模拟及应用研究 [J].北京理工大学学报,2018,38(10):1025-1029.
(SUN Bao-ping,GAO Wen-xue,ZHOU Shi-sheng.Study on numerical simulation and application of blasting of tunnel excavation [J].Transactions of Beijing Institute of Technology,2018,38(10):1025-1029.)
[10] 邵东辉,费鸿禄,杨朝阳,等.新建隧道爆破对既有隧道影响的数值模拟分析 [J].工程爆破,2017,23(5):67-70.
(SHAO Dong-hui,FEI Hong-lu,YANG Chao-yang,et al.Numerical simulation analysis of influence of new tunnel blasting on existing tunnel [J].Engineering Blasting,2017,23(5):67-70.)
[11] 吴能森.地下工程结构 [M].武汉:武汉理工大学出版社,2015.
(WU Neng-sen.Underground engineering structure [M].Wuhan:Wuhan University of Technology Press,2015.)
[12] 占城.城市隧道爆破震动对邻近建筑物的影响及安全评估 [D].重庆:重庆交通大学,2017.
(ZHAN Cheng.Damage evolution analysis and safety evaluation of the adjacent structure by urban tunnel blasting vibration [D].Chongqing:Chongqing Jiaotong University,2017.)
[13] 闫兵,黄华东,刘云,等.不同弹模工况下隧道爆破震动空洞效应的数值模拟研究 [J].公路,2016,61(5):226-231.
(YAN Bing,HUANG Hua-dong,LIU Yun,et al.Numerical simulation study on the hollow effect of tunnel blasting vibration under different elastic modulus [J].Highway,2016,61(5):226-231.)
[14] 陈阳.萨道夫斯基公式在城市地铁爆破施工中的运用 [J].黑龙江交通科技,2011,34(10):332-333.
(CHEN Yang.Application of Sadovsky formula in blasting construction of urban subway [J].Communications Science and Technology Heilongjiang,2011,34(10):332-333.)
[15] 李华,黄本才.结构内部爆炸空洞效应对超压影响的数值模拟 [J].工业建筑,2012,42(2):48-53.
(LI Hua,HUANG Ben-cai.The numerical simulation of influence of an internal blast cavity effect on overpressure for a structure [J].Industrial Construction,2012,42(2):48-53.)