随着我国经济水平的不断提升,食品品质受到了更多的关注[1-2].新零售概念的出现促进了现代物流行业的进一步快速发展,尤其是冷链技术与冷链物流技术的不断突破,极大地保障了生鲜电商的长久发展[3].
冷链物流是将冷冻工艺学与物流运输相结合,利用制冷及保温等技术手段以达到在低温或不同温度环境下运输货物的目的.通常,根据货物的种类、数量及运送距离的不同,冷链物流的形式也有所区别[4-5].在整个冷链物流过程中,路径优化问题是影响货物配送效率的最关键问题之一.在多温区冷链物流配送过程中,车辆路径的规划经常受到多种因素的约束,进而影响了多温区冷链物流的配送时间、配送成本和配送风险.多温区冷链物流的车辆路径规划可分为以下两类:1)仅针对单纯送货或者取货的车辆路径规划问题;2)送货、取货一体化的车辆路径规划问题[6-9].
目前,已有众多学者针对这一领域研究取得了一定成果.张济风、康凯、施文嘉等人通过分析我国冷链物流企业现阶段管理模式,总结出影响冷链物流发展的因素[10-12].孔志学等[13]利用最优分割法来确定第一级配送路径,从而确定了中转站的个数和位置,并在此基础上得到第二级配送路径.该方法能得到较高的日均转载率,但其缺点也较为明显:单车装载率较低.姜涛[14]在插入法中融入时差的概念,开展了带有时间窗约束要求、同时取送货配送车辆路径算法的研究.
本文在蚁群算法的基础上,融入了粒子群算法优势,构建面向多温区冷链物流的混合蚁群车辆路径优化算法,以此来解决带时间窗和同时取、送货的问题.
1 问题描述与建模
送货、取货一体化的车辆路径规划问题可简单理解为:在某个特定的配送中心派出多个配送车辆并为多个目标客户进行货物配送服务,且目标客户均有一定量的送货与取货需求.与单纯送货、取货车辆路径规划问题不同的是,送货、取货一体化的车辆路径规划问题还需要考虑任何目标客户的送货、取货综合需求不能超出该车辆的总运载能力Q.考虑到在实际物流配送过程中,通常受到一定的时间限制,因此带时间窗的同时取、送货车辆路径规划问题是更加具有现实意义的研究课题[15].本文采用两个种群混合策略,并进行线性结合,从而对多温区冷链物流的车辆路径优化模型构造初始可行解及局部搜索方法.
为了便于问题描述与模型构建,本文假定冷链物流过程仅考虑一个配送中心站点.该配送中心站点使用M辆运载能力为Q的配送车来满足n个客户的送货和取货任务,其中,配送车辆的行驶速度为固定值.带时间窗的同时取、送货车辆路径规划问题被描述成如下过程:1)若干辆配送车从配送中心站出发,完成取货、送货后再返回配送中心站;2)每一个客户均有一个取货点和送货点;3)配送车辆需在配送中心站装好货物后在规定的时间窗内将货物送达,并将客户的货物取回;4)车辆路径规划目标为配送站以最小的成本(选择最少的车辆使用费用、最短的行驶费用以及取货、送货服务费用)完成任务.
根据上述描述过程,使用V={0,1,…,n}来表示客户和配送站集合,其中,0代表配送中心站.假设U+代表取货节点集合,U-代表送货节点集合,而U为U+和U-的并集.c={1,2,…,M}表示参与冷链运输任务的车辆集合.分别使用Sij和dij来表示从节点i到节点j的行驶费用与行驶距离.节点i到节点j既可以表示取货节点,也可以表示送货节点,因此它们的取值范围为i=1,2,…,n和j=1,2,…,n.而ti表示在节点i进行服务所使用的时间,并且t0=0.使用[ei,li]来表示完成节点i任务的时间窗,其中,ei、li分别代表最早以及最晚开始工作的时刻.使用qi来表示配送车辆在节点i取完或送完货后的货物载重量.
根据以上假设,目标函数f被定义为
(1)
式中:表达式第一项为配送车辆的使用费用;第二项为车辆从节点i到节点j的行驶费用;第三项为在节点取货、送货的服务费用;a1、a2、a3分别为比例系数;Zijc为本次研究的决策变量,当某车辆c完成从节点i运行到节点j时,令Zijc=1,否则令Zijc=0;ti为配送车辆到达节点i的时刻.
为了保证配送车辆在指定的送货、取货节点完成先取货、再送货的工序,设定约束条件为
(2)
(3)
根据假设内容,所有车辆统一从配送中心开往客户地址进行服务,完成客户的取货、送货需求后再返回配送中心,由此得到对站点的约束条件为
(4)
(5)
考虑到配送车在执行任务时,受限于每个客户指定的时间进行送货、取货,因此需要增加时间窗对配送车的行为进行约束,即
(6)
式中,Uic、Dic分别为最佳服务时间的下限和上限.
2 同时取、送货车辆路径优化
由于同时取货、送货增加了路径优化问题的求解维度[16],为得到最优解,本文将粒子群算法在多维度搜索空间方面的优势与改进后蚁群算法相结合,以此来构造初始可行解及局部搜索方法.
2.1 蚁群算法的路径选择
选择合适的车辆行驶路径,即选择合适的客户.与客户之间的距离d和货物量是约束路径规划的因素,设置变量ηij来表征客户i、j被同一辆车服务的可能性,ηij被定义为
(7)
由于蚁群算法容易得到局部最优解,本文使用多样性搜索与确定性搜索相结合的方式来规避蚁群算法正反馈的影响,具体表达式为
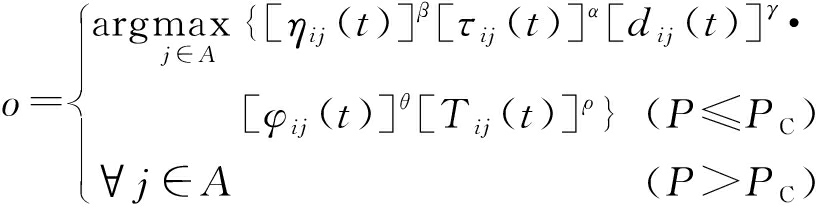
(8)
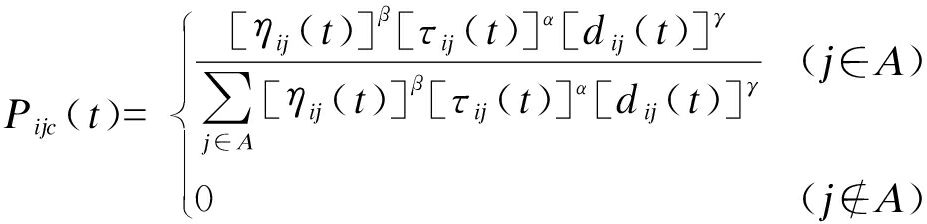
(9)
式中:τij(t)为在t时(i,j)上的信息素;Pijc(t)为蚂蚁c从节点i转移到节点j的可能性;α为信息素的启发因子;β为某节点客户被选中的期望因子;PC为选择概率,在蚂蚁种群迭代过程中该值会发生改变;γ为缩小车辆行驶距离的必要性;θ为车载量与用户取货、送货匹配程度φij的权重;ρ为赶往下一客户的紧迫程度Tij的权重;A为可选择的客户节点集合.P处于[0,1]之间且均匀分布,当P≤PC时,为确定性搜索;当P>PC时,则为多样性搜索.
2.2 带时间窗的同时取、送货车辆路径优化算法求解
尽管蚁群算法可作为路径优化算法进行路径规划,但其劣势也不容忽视:1)在进行可行解优化的过程中容易得到局部最优解;2)优化过程时间较长.针对以上两个问题,利用粒子群算法寻求最优解方面的优势,来减少最优解搜索时间,并缩小求解空间以提高算法效率.粒子群算法的核心在于利用粒子的当前位置信息、全局极值以及个体极值,规划出粒子下一次迭代后的位置信息.
将基于蚁群算法路径规划的4个参数α、β、ρ、γ作为粒子群的一个粒子,粒子的位置及速度可与参数相互转.粒子群算法在优化过程中,惯性权重会影响全局搜索的能力.当惯性权重较大时,可增强算法的全局搜索能力.通过粒子位置得到粒子参数后,初始化蚂蚁子群的信息素,并计算相邻位置节点之间的距离和车辆行驶时间.当蚂蚁经过一条边时,会更新该条边上的信息素,具体更新表达式为
τ′ij=(1-ξ)τij+ξτ0
(10)
式中:ξ为信息素挥发率;τ0为初始信息素.
本文使用插入操作来构建带时间窗,同时取、送货车辆路径问题的弱可行解,即随机选择一个客户作为第一位要服务的目标,在进行第二名客户服务之前,从满足服务要求的客户集合V中随机挑选一个客户k插入到正在进行的路径当中.该客户的插入,引发了信息素的变化,并按照车辆已装载的容量和剩余容量来更新节点的最大服务量.
若客户k与配送中心的距离在插入k之后路径长度的变化会影响路径规划效果,那么当集合V中无可插入的客户时,则路径即完成规划.在进行一次迭代后,求出每只蚂蚁的路程Lc,由此得到蚂蚁子群的局部最优解为![]()
为避免蚁群算法因收敛速度过快而得到局部最优解,本文使用交叉、反转来优化蚁群个体.在经过交叉、反转等操作后,求出在满足时间窗等约束条件下的最优路径方案Lopt.
交叉操作是指随机选择可行解中两条路线r1、r2,将路线重叠的部分连接,保留对路线优化有改善效果的交叉组合;而反转则是调转车辆的行驶方向,在不改变行驶路线长度的情况下,减少车辆装载重量.
取Llocal、Lopt两者最大值作为Llocal最新值,而该子群粒子的适应值被设定为蚂蚁子群的最优路径,并更新蚂蚁个体自身的最优解,进而更新粒子的位置和速度.当所有子群蚂蚁均得到局部最优解后,信息素更新表达式为
(11)
式中:Cbest、Cworst为子群蚂蚁寻找到的最优及最差路径;W为相关系数.在所有子群信息素更新完成后,进行子群之间的信息素矩阵交换,得到交换数组,并进行交换操作.当满足终止约束条件时,即得到全局最优解.
3 实验分析
为验证本文所述方案的有效性和可行性,利用Visual C++6.0、MATLAB 7.0仿真平台对基于混合蚁群的多温区冷链物流配送路径优化算法进行验证.实验使用大小为200单元×200单元的平面区域进行路径规划.为比较本文所提算法(M1)的综合性能,设置对照组进行验证.对照组为基于改进的遗传算法的车辆路径优化算法(M2)和基于禁忌搜索算法的车辆路径优化算法(M3).基于改进的遗传算法车辆路径优化算法将传统遗传算法的交叉、变异操作进行改进,根据目标函数值的大小来划分配对的个体;再基于给定的变异率,对个体相应位置的基因进行变异.将变异从交叉操作中分离出来,提高算法的效率.基于禁忌搜索算法的车辆路径优化算法通过试探一系列的特定搜索方向,让特定的目标函数值提高到最大的程度,从而避免进入局部最优解.
文中所述混合蚁群算法的参数设置如下:车辆数目M为20,初始粒子参数值α、β、ρ、γ分别为1、3、0.2、0.25,θ=1.遗传算法的基本参数设置为:种群个体数量为100,迭代次数30次.
实验测试对象为装载量较小、时间窗较窄的冷链物流运输站,分别面向10个客户、25个客户以及50个客户进行取、送货服务,测试实验进行两次,且两次客户的坐标不同.
首先针对车载量较少,时间窗较短的配送场景进行试验.表1分别展示了3种算法在配送车辆NV、路径规划时间CT和配送总距离TD方面的对比.
表1 3种路径规划算法对比
Tab.1 Comparison among three path planning algorithms
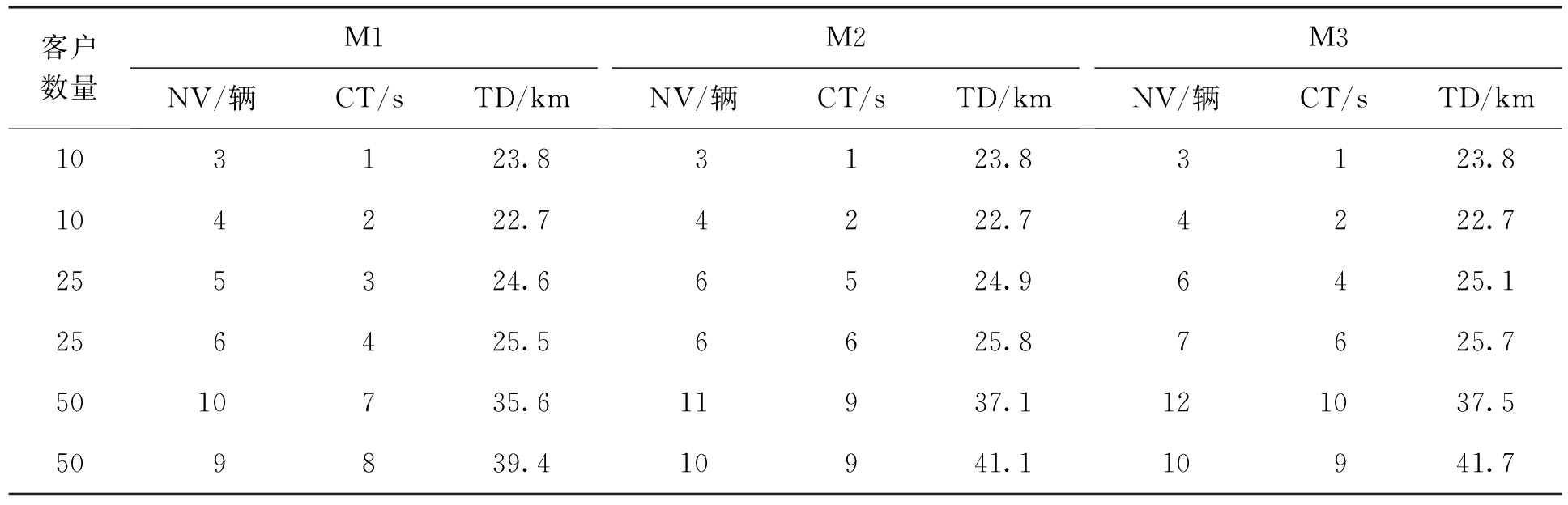
客户数量M1NV/辆CT/sTD/kmM2NV/辆CT/sTD/kmM3NV/辆CT/sTD/km103123.83123.83123.8104222.74222.74222.7255324.66524.96425.1256425.56625.87625.75010735.611937.1121037.5509839.410941.110941.7
从表1可以看出,与M2算法及M3算法相比,当客户数量为10时,本文所提算法(M1)与另外两种算法综合性能相同;而当客户数量增长为25和50时,基于混合蚁群算法用于路径规划的平均时间要优于对照组,且所派出的车辆数量较少,配送距离也更短.
测试实验增加了不同客户数量时配送总成本的验证.根据上文的分析,配送总成本包含了配送车辆使用费用、车辆行驶费用以及取货、送货服务费用.结合目标函数表达式,客户数量会影响到配送车辆数量、车辆行驶距离和服务时间的比例系数.在经过混合蚁群算法转化后,最终优化参数为:α∈[1,2]、β∈[3,5]、ρ∈[0.3,0.6]和γ∈[0.1,0.3],para={α、β、ρ、γ},且搜索空间的维度为4.粒子下界、上界分别为paramin={1,3,0.3,0.1}、paramax={2,5,0.6,0.3}.测试结果见图1所示.
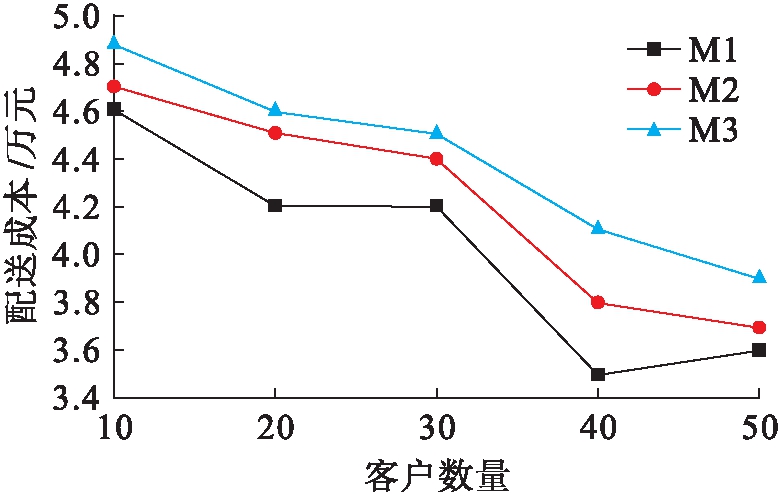
图1 3种优化算法在不同客户数量下配送总成本对比
Fig.1 Comparison of total distribution cost among three optimization algorithms under different customer numbers
图1中随着客户数量的增加,本文所提算法的配送总成本均低于对照算法.原因在于M2算法中遗传算法的收敛速度较慢;而M3算法中禁忌搜索算法依靠禁忌表来避免进入局部最优解,当客户数量较多时,出现循环求解的几率也随之增加.值得注意的是,当客户数量从40增加50时,M1算法的配送成本有所增加.因为车辆的装载量较少,为满足同时取、送货的要求,则需更多的车辆来完成配送任务.
图2展示了3种路径优化算法在客户数量一定情况下的总成本与收敛速度.从图2可以看出,随着迭代次数的增加,3种路径优化算法的配送总成本均呈现下降的趋势.其中,本文所提算法的总成本明显低于对照算法,收敛速度分别提高了24.3%和18.6%,表明基于混合蚁群的路径优化算法的优越性.本文将影响车辆路径规划的α、β、ρ、γ参数转化为粒子优化算法中的粒子,粒子群优化算法的应用增强了蚂蚁子群对最优解的寻找能力,并在蚂蚁子群之间交换信息素可避免子群得到局部最优解,同时通过插入的启发形式来求解弱可行解,从而增强了算法的性能.
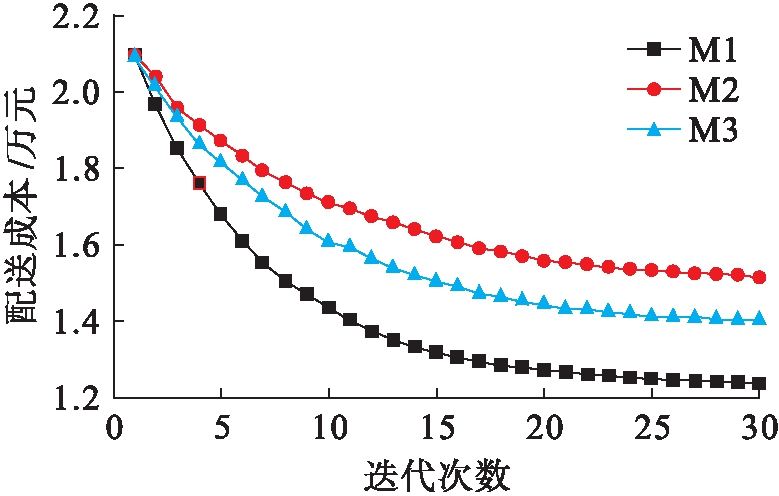
图2 3种路径优化算法的总成本和收敛速度
Fig.2 Total cost and convergence speed of three route optimization algorithms
4 结 论
为满足同时取、送货这一复杂的市场需求,在考虑时间窗的情况下,提出了基于混合蚁群的多温区冷链物流配送路径优化算法.通过将粒子群与蚁群算法相结合,增强蚂蚁子群对路径优化最优解的探索能力.同时采用基于插入的启发式方法构造弱可行解,并以交叉、反转来提高求解收敛速度.对照实验表明,该算法有效降低了迭代次数并提高了收敛速度.
[1] 范立南,董冬艳,李佳洋,等.基于生鲜农产品的冷链物流配送路径优化 [J].沈阳大学学报(自然科学版),2017,29(2):125-131.
(FAN Li-nan,DONG Dong-yan,LI Jia-yang,et al.Route optimization of cold chain logistics based on fresh agricultural products [J].Journal of Shenyang University (Natural Science),2017,29(2):125-131.)
[2] 钱嘉琪,赵欣瑶,孙雪.低碳视角下车辆的物流配送路径优化问题研究 [J].科技经济导刊,2021,29(2):27-28.
(QIAN Jia-qi,ZHAO Xin-yao,SUN Xue.Research on the optimization of vehicle logistics distribution route from the low-carbon perspective [J].Technology and Economic Guide,2021,29(2):27-28.)
[3] 尹枭.基于蚁群算法的冷链物流配送路径优化及系统实现 [D].哈尔滨:哈尔滨工业大学,2017.
(YIN Xiao.Route optimization and system implementation of cold chain logistics distribution based on ant colony algorithm [D].Harbin:Harbin Institute of Technology,2017.)
[4] 丁艳.多温共配冷链物流车辆配送路径优化仿真 [J].沈阳工业大学学报,2021,43(3):311-316.
(DING Yan.Simulation of vehicle distribution path optimization for multi-temperature co-distribution cold chain logistics [J].Journal of Shenyang University of Technology,2021,43(3):311-316.)
[5] 张秀萍,易金聪.基于GPS的冷链物流监控终端的设计与实现 [J].计算机应用与软件,2018,35(4):182-186.
(ZHANG Xiu-ping,YI Jin-cong.Design and realization of cold chain logistics monitoring terminal based on GPS [J].Computer Applications and Software,2018,35(4):182-186.)
[6] 吕成瑶,邵可南,张帅帅,等.生鲜食品冷链物流配送路径优化 [J].计算机技术与发展,2020,30(11):168-173.
(LÜ Cheng-yao,SHAO Ke-nan,ZHANG Shuai-shuai,et al.Optimization of fresh food cold chain logistics distribution route [J].Computer Technology and Development,2020,30(11):168-173.)
[7] 叶威惠,张飞舟.真实路况下的快递配送路径优化研究 [J].计算机工程与科学,2017,39(8):1530-1537.
(YE Wei-hui,ZHANG Fei-zhou.Express distribution route optimization under real-time road condition [J].Computer Engineering & Science,2017,39(8):1530-1537.)
[8] 任腾,陈玥,向迎春,等.考虑客户满意度的低碳冷链车辆路径优化 [J].计算机集成制造系统,2020,26(4):1108-1117.
(REN Teng,CHEN Yue,XIANG Ying-chun,et al.Optimization of low-carbon cold chain vehicle path considering customer satisfaction [J].Computer Integrated Manufacturing Systems,2020,26(4):1108-1117.)
[9] 陈立伟,唐权华.基于Memetic算法的两级车辆路径优化 [J].重庆大学学报,2017,40(3):95-104.
(CHEN Li-wei,TANG Quan-hua.Two-echelon vehicle path optimization based on Memetic algorithm [J].Journal of Chongqing University,2017,40(3):95-104.)
[10] 张济风,杨中华.时变路网环境下多温冷链配送路径优化研究 [J].重庆师范大学学报(自然科学版),2020,37(1):119-126.
(ZHANG Ji-feng,YANG Zhong-hua.Research on distribution path optimization of multi-temperature cold chain in time-varying road network environment [J].Journal of Chongqing Normal University (Natural Science),2020,37(1):119-126.)
[11] 康凯,韩杰,普玮,等.生鲜农产品冷链物流低碳配送路径优化研究 [J].计算机工程与应用,2019,55(2):259-265.
(KANG Kai,HAN Jie,PU Wei,et al.Optimization research on cold chain distribution routes considering carbon emissions for fresh agricultural products [J].Computer Engineering and Applications,2019,55(2):259-265.)
[12] 施文嘉,邵竑湄,唐迪,等.基于优化免疫算法冷链物流配送路径研究 [J].微型电脑应用,2019,35(12):103-107.
(SHI Wen-jia,SHAO Hong-mei,TANG Di,et al.Research on cold chain logistics distribution route based on optimized immune algorithm [J].Microcomputer Applications,2019,35(12):103-107.)
[13] 孔志学,姜恒,张珠峰.改进蚁群算法在生产线加工方案选择中的应用 [J].航天制造技术,2021(4):17-23.
(KONG Zhi-xue,JIANG Heng,ZHANG Zhu-feng.Application of improved ant colony optimization in production line processing planning [J].Aerospace Manufacturing Technology,2021(4):17-23.)
[14] 姜涛.基于模式融合的网络动态资源柔性调度仿真 [J].计算机仿真,2021,38(6):330-334.
(JIANG Tao.Flexible scheduling simulation of network dynamic resources based on mode fusion [J].Computer Simulation,2021,38(6):330-334.)
[15] 张家波,袁凯,吴昌玉.一种基于链路质量的蚁群优化VANET路由算法 [J].重庆邮电大学学报(自然科学版),2020,32(2):185-191.
(ZHANG Jia-bo,YUAN Kai,WU Chang-yu.An ant colony optimization routing algorithm based on link quality for VANET [J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2020,32(2):185-191.)
[16] 刘艳秋,吴蒙,徐世达.考虑不可行路径的逆向物流回收路径问题 [J].沈阳工业大学学报,2016,38(4):416-420.
(LIU Yan-qiu,WU Meng,XU Shi-da.Reverse logistics recovery path problem with considering unfeasible path [J].Journal of Shenyang University of Techno-logy,2016,38(4):416-420.)