结构的损伤识别作为结构健康监测中的重要内容,能够为结构剩余寿命评估提供重要参考依据,有较高的研究价值.近年来,有关结构损伤识别方法的种类繁多,成果丰硕[1-3].很多学者将结构信息与不同算法相结合并应用于实际工程的损伤诊断中,这印证了损伤识别的指标及方法存在更高精度、更高效的趋势[4-6].在这些方法中,将结构动力指纹与神经网络算法相结合的成果较为丰硕[7-8].对于受弯构件,曲率模态及其变形形式具有较高的精度及适用性,且其结合神经网络已被证明可以较好地识别损伤,但仍存在以下问题:曲率模态在靠近振型节点处精度不高;需要较密集测点,实际工程中难以实现;利用曲率模态差等指标进行损伤识别需要结构未损伤数据,对部分既有桥梁难以实现.
信息熵作为控制论等领域的重要概念,在土木工程领域仍处于初步研究阶段.Li等[9]将信息熵与结构模态位移相结合,利用神经网络及信息融合技术提高了损伤识别的精度;程建曙[10]将信息熵用于混凝土裂缝扩展机理的描述;丛培江等[11]阐明了“能量熵”的概念并解释了其在土木工程应用的原理.在此基础上,Yang等[12-13]将结构的模态看作波形并将基于模态位移的广义局部信息熵应用于梁式结构的损伤识别中,结果证明该指标优于模态位移指标.
本文针对曲率模态的不足,结合信息熵具有的较大研究潜力,对曲率模态进行必要的改进和扩展,提出“模态信息熵”的概念使其可以弥补上述缺陷.通过有限元算例结合神经网络对损伤进行定位、定量以验证指标的有效性,最后通过损伤钢梁模态测试,结合神经网络进行实际结构损伤识别以验证指标的实用性.
1 广义局部曲率模态信息熵
1.1 指标引入及推导
对于离散变量,设信号长度为n,信号i的信息量为xi,则信息熵可表示为
H(X)=E[I(xi)]=E[-logapi]=
(1)
式中:I(xi)为xi所代表的自信息量;E[I(xi)]为所有自信息量的数学期望;pi为信号i出现的概率;下标a通常取e.
节点所包含的信息可以看作是相互独立的信息源.因此,本文在通过信息熵来表征结构损伤的情况下,结构包含的信息可看作离散变量.桥梁的模态位移或其变形形式均可视为波形,其局部的复杂性可以通过熵进行估计,称为“模态熵”.当波形较为平滑时,熵的变化幅值较小,而当波形突变时,熵的变化幅度大,本文即以此原则识别损伤.若信号i的各个部分所包含的信息量相等时,各信号局部概率之和为1,且每个信号的信息熵为![]() 此时则有pimax=1/n.
此时则有pimax=1/n.
对于广义局部信息熵,各个信号的和并不等于1,且利用测点i及其周围测点的振动信号直接代表该测点所包含的信息量.基于以上考虑,并不能将该指标称作经典意义上的信息熵,称其为“广义”;又因该指标侧重于表征测点所包含信息量占附近节点信息量的比重,因此称其为“局部”.该指标能够进行损伤识别的依据为:若该信号的长度中各个单位信号所包含信息量相等,不难证明pimax=1/n.该特性反映到结构中则表现为:若结构无损伤,结构各个节点包含的信息量处处相等,指标平滑;若结构出现损伤,则损伤位置出现峰值,可定位损伤.
根据“模态熵”的概念,将结构的模态位移视作波形,结合曲率模态能够定位、定量损伤的优势,本文构造计算点i的广义局部曲率模态信息熵的局部概率pi时,取i点和前后紧邻的点共N个(N为正奇数且N≥3),并以每个点的曲率模态vi代表该点的信息量,则此时定义局部概率为
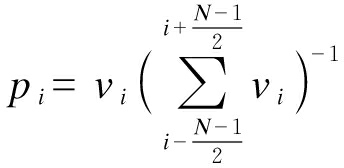
(2)
(3)
式中:yi为i点的模态位移;h为测点间距.本文利用式(3)计算简支梁桥的曲率模态.i点的广义局部曲率模态信息熵可表示为
HGLvi=-piln pi
(4)
1.2 概率窗口选取
式(2)中,N为参与计算的点,宏观上为滑动计算窗口.N的取值越大,则参与计算的点越多,对于曲率模态,微小损伤造成的结构特性变化有可能会埋没在庞大的结构信息里而无法表征,且滑动窗口可能包含不同测点的多个损伤信息,这使得窗口中所反映的损伤信息不完整,从而影响损伤识别的精度.同时,N的取值越大,则计算中结构两端因数据缺失,不满足式(2)计算要求的点越多.综上,N的取值不宜过大.本文取N=3,可得
(5)
联合式(3)~(5)并结合信息熵定义,可得到结构模态位移(各阶振型分量)与广义局部曲率模态信息熵的关系为
(6)
本文利用式(6)计算前两阶广义局部曲率模态信息熵并以此指标对结构进行损伤识别.简支梁的二阶竖向振型跨中存在振型节点,其存在使得损伤识别易发生误判,因此有必要对该条件下损伤识别的指标进行改进.
1.3 指标改进
本文针对二阶振型即跨中存在振型节点的振型进行改进,探究利用其进行损伤识别的可行性.限于篇幅,简支梁的三阶及更高阶广义局部曲率模态信息熵的计算方法及损伤识别可针对本文研究内容进行类比,此处不再赘述.
利用这类振型数据进行损伤识别时,根据式(4)、(5)则有
(7)
(8)
式中:t为有限元单元划分的个数;p0为跨中振型节点处的局部概率;HGLv0为该处的广义局部曲率模态信息熵.由式(8)可知,若曲率模态包含此类振型节点,则广义局部曲率模态信息熵会有明显的趋于0的峰值,容易使判别损伤位置时发生误判.为了避免该情况发生,需对曲率模态进行处理,处理的依据为:曲率模态无单位且为承弯结构振动特性的特殊表现形式,其表达式为
(9)
则有
(10)
式中:y′i为第i点的结构竖向振型分量;v′i为第i阶变形前的结构曲率模态.处理后能够有效地规避二阶指标产生趋于0的峰值,且移轴后结构的振动趋势未发生改变.
2 简支梁数值模拟算例
2.1 MIDAS模型建立
以一混凝土简支梁桥为例,该桥的全长L=32 m,设计截面为箱形截面,如图1a所示(单位:mm),单元属性为梁单元,其中主梁结构采用C50混凝土,弹性模量为3.45×107 kN/m2,容重为25 kN/m3,泊松比为0.2.利用有限元软件MIDAS/Civil建立简支梁有限元模型,如图1b所示,该简支梁沿长度方向划分为等长的32个单元.
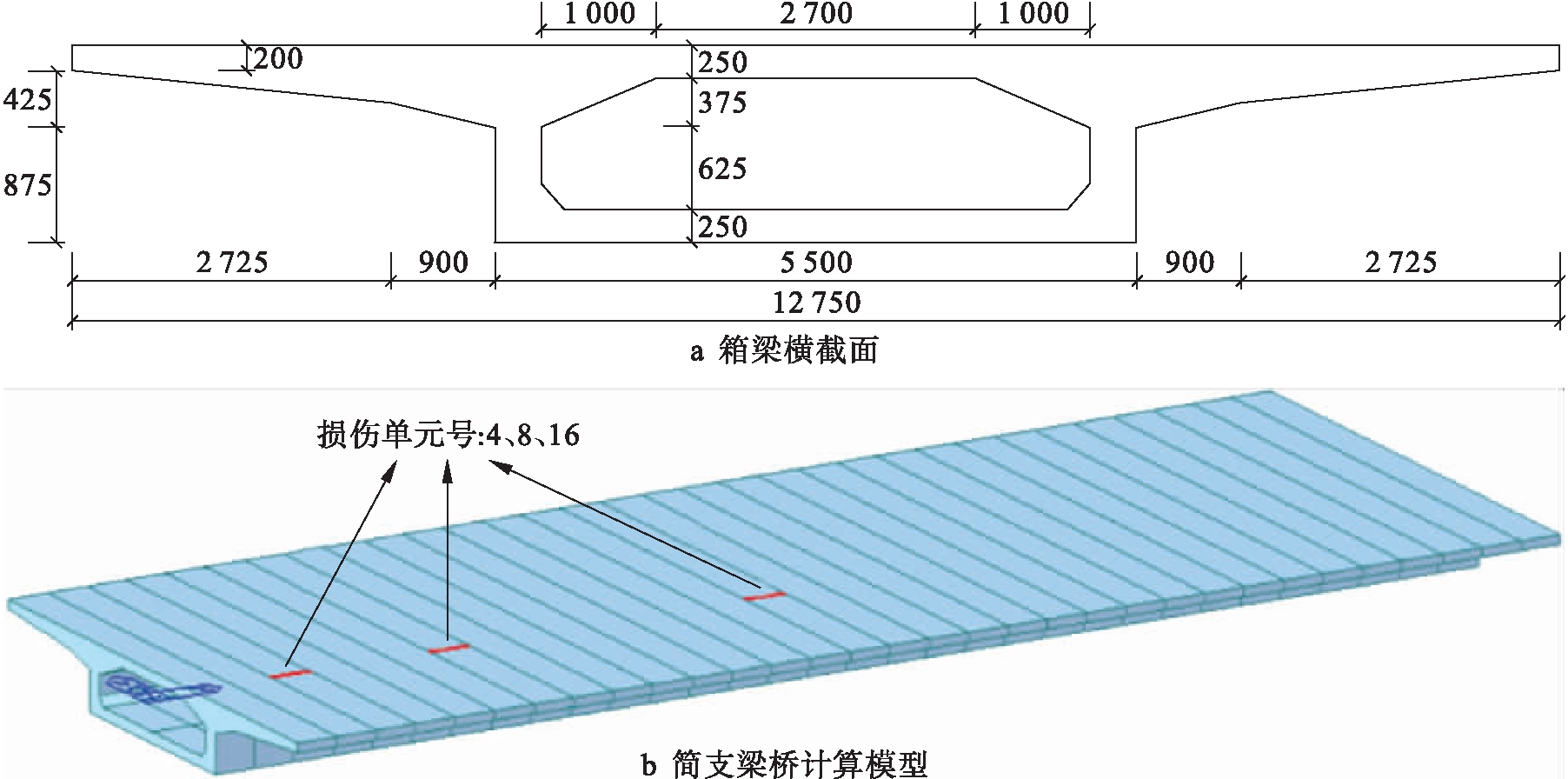
图1 简支梁桥几何构造及分析模型
Fig.1 Geometric structure and analysis model of simply supported beam bridge
为了验证指标的有效性,利用刚度折减法,通过弹性模量E的下降来模拟损伤,三个工况的损伤位置分别位于跨中、1/4跨和1/8跨,对应的损伤单元号为4、8、16,损伤程度均为20%,如表1所示.
表1 有限元模型损伤工况
Tab.1 Damage conditions of finite element model

损伤程度%损伤单元No.16损伤单元No.8损伤单元No.420工况1-1工况1-2工况1-3
2.2 指标损伤定位结果
简支梁桥模型中有共计29个可计算测点.提取一阶竖向振型并利用式(6)计算工况1-1至1-3结构各个节点的前两阶广义局部曲率模态信息熵,图2为前两阶广义局部曲率模态信息熵损伤识别结果.
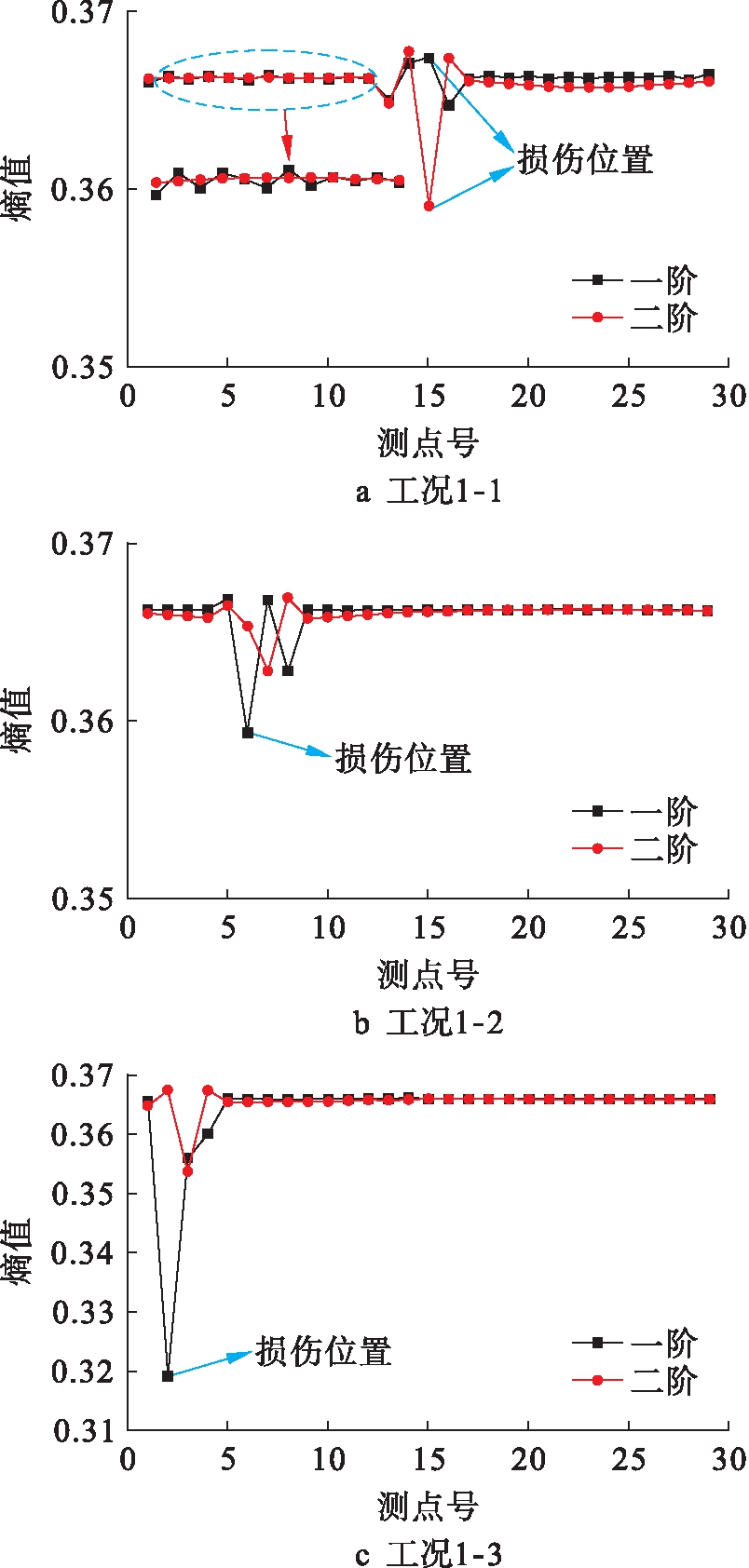
图2 前两阶广义局部曲率模态信息熵损伤识别结果
Fig.2 Damage identification results of first two order generalized local curvature modal information entropy
对于简支梁,一阶振型节点位于两端支座处,二阶振型节点位于简支梁跨中.二阶广义局部曲率模态信息熵在该阶振型节点(跨中)处损伤识别效果优于一阶指标,其峰值更明显.但随着损伤位置远离二阶振型节点,靠近一阶振型节点即支座处,一阶广义局部曲率模态信息熵峰值较二阶更为明显.说明不同阶数的广义局部曲率模态信息熵具有相同的性质,自阶振型节点处对损伤较其他位置敏感.
在跨中位置,前两阶指标均可以准确地定位损伤.在1/4跨及靠近支座的1/8跨处,二阶指标峰值较实际损伤位置有一个测点的偏移,但仍可以确定损伤的大致范围.随着单元网格划分精度、单元数量的提升,可以减少该现象对损伤识别的影响;同时,二阶广义局部曲率模态信息熵较一阶更为平滑.
2.3 基于神经网络的损伤定量方法及验证
对工况1-1至1-3进行损伤定量时采用三层BP神经网络,根据损伤定位结果,取已知损伤位置附近3个节点的广义局部曲率模态信息熵和曲率模态作为神经网络的输入参数,并构造三种损伤位置下损伤程度为10%、15%、25%、30%的共计12个工况作为两种指标的训练样本.根据三分法[14]试算神经网络的最优隐含层节点数为5,输出参数设置为损伤单元的残余刚度[οi],神经网络的构造均为3-5-1,各个网络训练最大迭代步数均为50,训练精度均为10-7.得到的损伤识别结果如表2所示.
由表2可知,在同样的神经网络参数下,前两阶曲率模态损伤定量的精度随着损伤位置靠近振型节点而降低.对于一阶曲率模态,在靠近支座的1/4跨和1/8跨处,损伤识别的相对误差达到了4.88%和8.25%;广义局部曲率模态信息熵损伤定量相对误差仅为4.13%和1.38%;二阶振型节点即简支梁跨中处二阶广义局部曲率模态信息熵损伤程度识别结果误差较小,相对误差仅为1.1%,但若损伤位置在远离振型节点的1/8跨处,其损伤程度识别相对误差达到了9.12%,高于曲率模态.因此,两种指标在识别位置不同的损伤时有互补的特点.
表2 神经网络损伤定量识别结果
Tab.2 Quantitative damage identification results of BP neural network
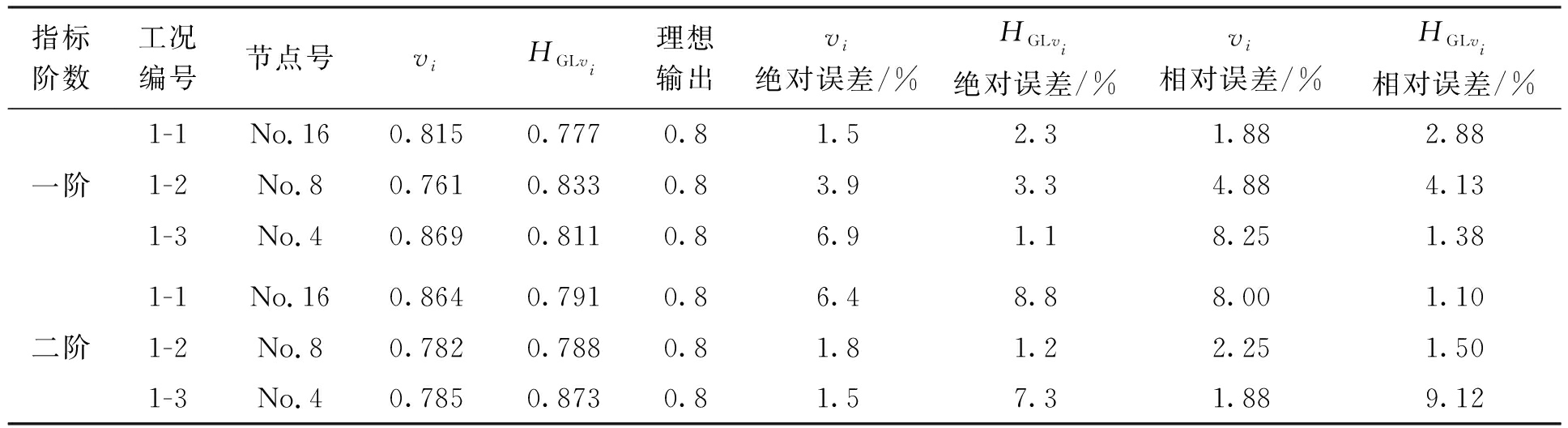
指标阶数工况编号节点号viHGLvi理想输出vi绝对误差/%HGLvi绝对误差/%vi相对误差/%HGLvi相对误差/%一阶二阶1-1No.160.8150.7770.81.52.31.882.881-2No.80.7610.8330.83.93.34.884.131-3No.40.8690.8110.86.91.18.251.381-1No.160.8640.7910.86.48.88.001.101-2No.80.7820.7880.81.81.22.251.501-3No.40.7850.8730.81.57.31.889.12
2.4 测点数量与指标识别效果的关系
利用曲率模态进行损伤识别时往往需要数量较多的测点,以便能够利用差分法进行计算.为了对实际工程及模态测试的测点布置提供一定参考,以简支梁模型为数值算例,将模型单元精细划分为64和128个,以模拟测点数量的增加.以一阶振型为研究对象,不同损伤程度下简支梁损伤识别结果如图3所示.
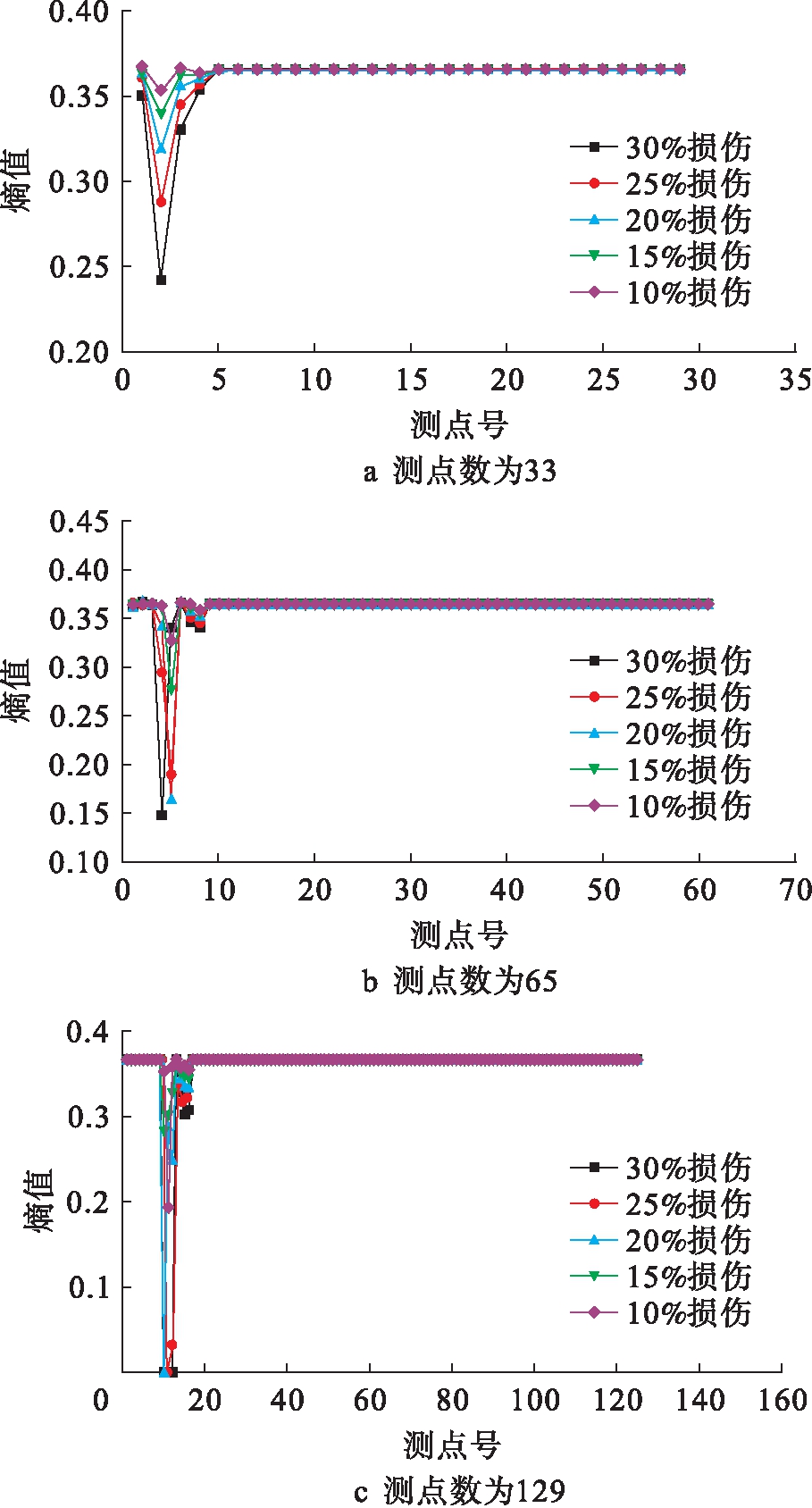
图3 不同测点数下1/8跨损伤识别结果
Fig.3 Damage identification results of 1/8 span with different number of measuring points
由图3可以看出,不同损伤位置下,节点在数量为33时损伤识别结果清晰,损伤位置处表征损伤的指标峰值较为明显.随着损伤程度的增加,其熵值减小并呈一定规律;但在测点数量为129时,损伤处有无法计算的熵值,且峰值处数值相差较大,损伤指标较不规律;能够对损伤进行定位,但无法进行定量损伤.指标在测点数量增多时呈现的不规律性对利用神经网络判定其损伤程度较为不利.本文中测点数为33时识别效果最佳.
综上所述,广义局部曲率模态信息熵在测点数量的选择上不同于曲率模态,该指标能够较好避免曲率模态需要密集测点这一缺点,即无需密集测点即可获得较好损伤识别结果.
3 试验验证
3.1 试验目的
为了进一步对本文所提出的广义局部曲率模态信息熵、损伤定量识别方法、精度及应用于实际工程中的识别结果进行考量和验证,基于上文对新损伤指标的研究和总结,本文将该指标应用于实际结构,通过对比试验和数值模拟识别结果验证该方法的可行性和实用性,以期为该指标及方法在实际工程中的应用提供一定的建议.
3.2 试验对象及测试设备
以钢梁为试验对象,钢梁横截面尺寸及设计为:钢梁梁体总长2 350 mm,计算跨径1 750 mm,净跨径1 650 mm,截面尺寸100 mm×8 mm.为了与试验室支墩紧密贴合,距离钢梁两端250 mm处设有长度为100 mm,截面尺寸为160 mm×8 mm的平面,螺栓固定位置位于钢梁净跨径两侧,预制螺孔以固定钢梁,与下方支座用螺栓连接.两支座中心间距为计算跨径,钢梁具体尺寸如图4所示(单位:mm),命名为钢梁-1.对钢梁进行材性试验,测得该钢材的平均屈服强度约为432 MPa;通过材性测定数据,计算其弹性模量约为1.989×105 N/mm2.

图4 钢梁尺寸
Fig.4 Steel beam dimension
除去支墩、支座底板及螺栓若干,采集系统及加速度传感器如图5所示.

图5 加速度传感器及采集分析系统
Fig.5 Acceleration sensor and acquisition analysis system
3.3 试验工况设置
钢梁-1为预制无损梁,无损梁测试完毕后返厂加工并于30 cm处(以支座中心为原点)开口2.5 cm,定为损伤工况3-1,测试完毕后在87.5 cm处开口2.5 cm,定为损伤工况3-2.实际开口形式如表3所示.
表 3 钢梁损伤工况
Tab.3 Damage conditions of steel beam

试件工况损伤情况钢梁-13-130cm处开口2.5cm3-287.5cm处开口2.5cm
3.4 测试方法及测点布置
测点无需布置过于密集,但其数量应保证能够识别损伤,结合传感器底座大小及钢梁实际情况,测点间距设为5 cm,进行数据分析时假定两支座中心处振型分量与理论值相等,值为0.全梁共34个测点,其中测点1位于距固定铰支座中心5 cm处.测点34位于距滚动支座中心5 cm处,其余各个测点均匀分布.
试验采用锤击法进行模态数据采集.试验室共有6个高频加速度传感器,为了测得同一工况下结构完整的振型,以5个测点及1个参考点为一组进行测试,共需7组测试.通过力锤对参考点附近进行激励以触发采样,每组采样采集三次,取平均值进行分析.
试算结果表明,结构的一阶振型峰值最大处在跨中部位,但该位置恰好为二阶振型节点.结构的二阶振型在3/4处达到峰值且与一阶振型方向相反.基于上述考虑,本文试验中获取结构的一阶振型时,将参考点设立在测点18处.获取结构二阶振型时,则将参考点设立在靠近3/4处(131.25 mm)附近的测点26处.具体的测点分布形式如图6所示(单位:mm).
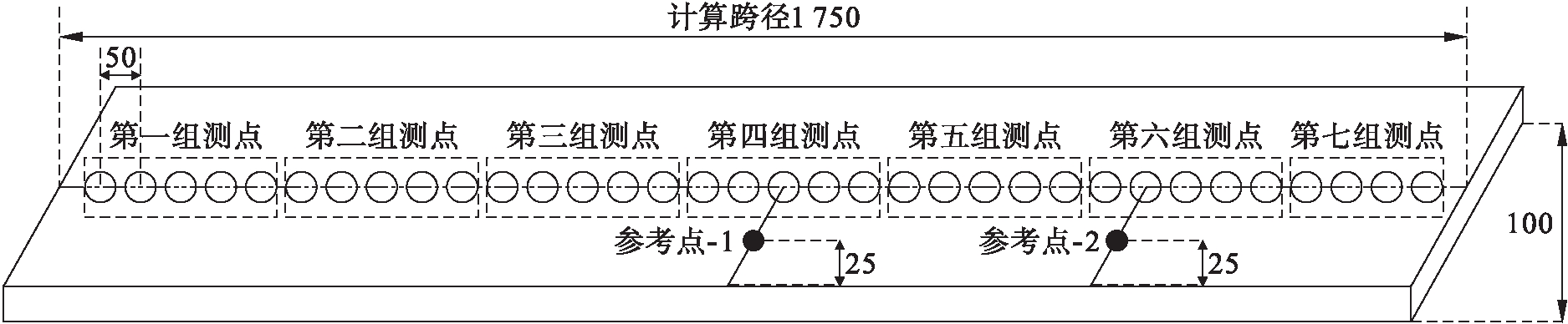
图6 模态测试测点布置图
Fig.6 Layout of modal measuring points
针对前两阶模态,加速度响应采集完毕后,利用随机子空间分析法分析采集到的波形时域数据,以参考点为基准进行振型归一化和质量归一化处理,提取前两阶竖向振型分量.最后对数据进行滤波预处理,确定损伤识别结果.试验采集现场及采集过程如图7所示.

图7 模态测试现场
Fig.7 Modal test site
3.5 试验结构有限元模型
为了与实际试验模型进行有效对比分析,确定试验数据的准确性,采用MIDAS/Civil和ANSYS两种有限元软件根据试验对象的实际尺寸建立相应有限元模型.
MIDAS/Civil全模型沿梁方向共计235个长度为1 cm的梁单元,共2 350 mm.同时利用ANSYS进行实体单元建模,单元类型为solid185.选用六面体单元对模型进行扫掠划分,网格大小选用4 mm.根据材性试验结果对两模型中单元赋予材料属性,弹性模量为1.989×105 N/mm2,泊松比为0.3,容重为7.698×10-5 N/mm3.具体模型如图8所示(以工况3-1为例).
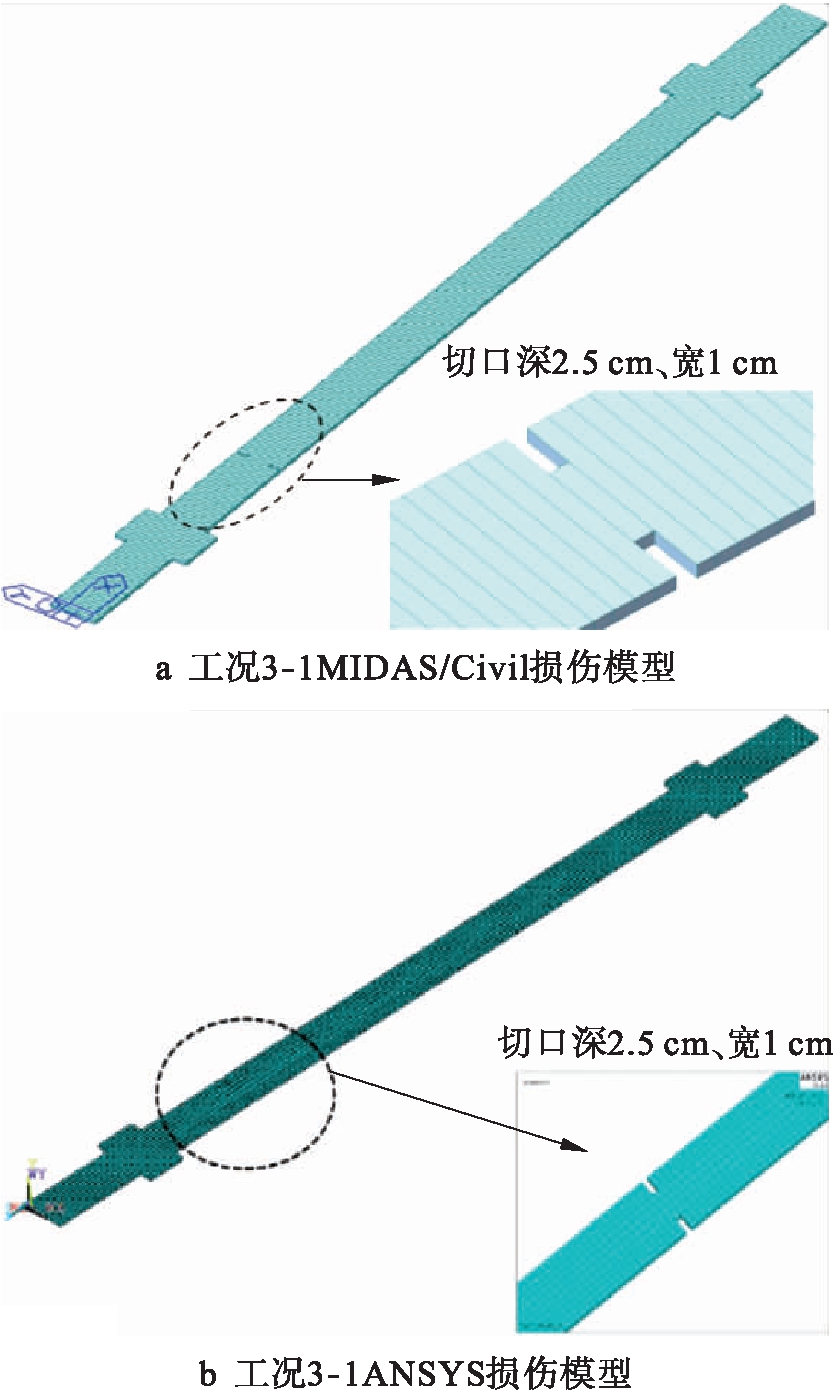
图8 有限元损伤模型
Fig.8 FEM damage model
分别进行模态分析,得到结构的前两节实测振型,并将ANSYS、MIDAS和实测振型进行归一化处理.将得到的振型代入式(3)~(10)计算结构的前两阶曲率模态及广义局部曲率模态信息熵.损伤识别结果如图9所示.
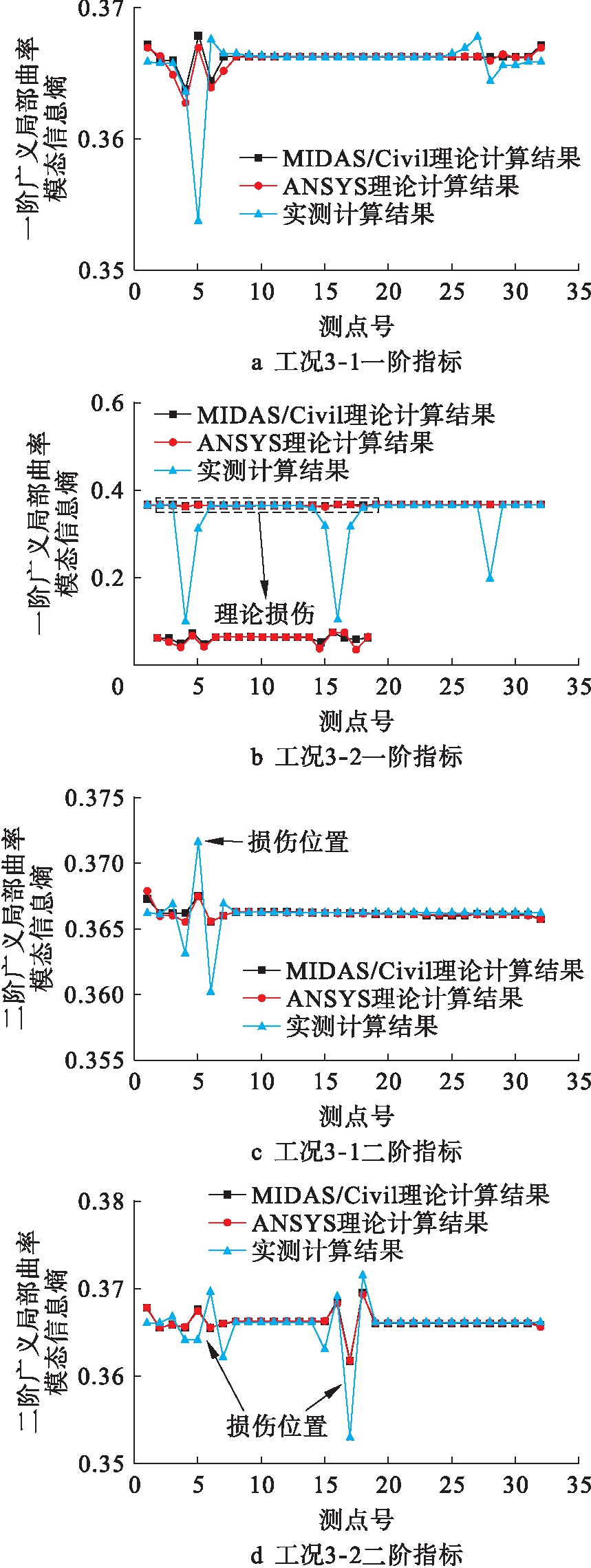
图9 指标实测、理论损伤位置
Fig.9 Actual and theoretical damage index locations
损伤定量神经网络依旧采用三层BP神经网络,并构造两个损伤位置下开口深度为1.5、2.0、2.5、3.0 cm(含同时损伤)共计18个工况作为两种指标的训练样本.各项参数的选取与上一节神经网络相同,输出函数为该单元的残余刚度[oi].确定隐含层最优节点数为11,因此,神经网络的构造为3-11-1.损伤定量结果如表4所示.
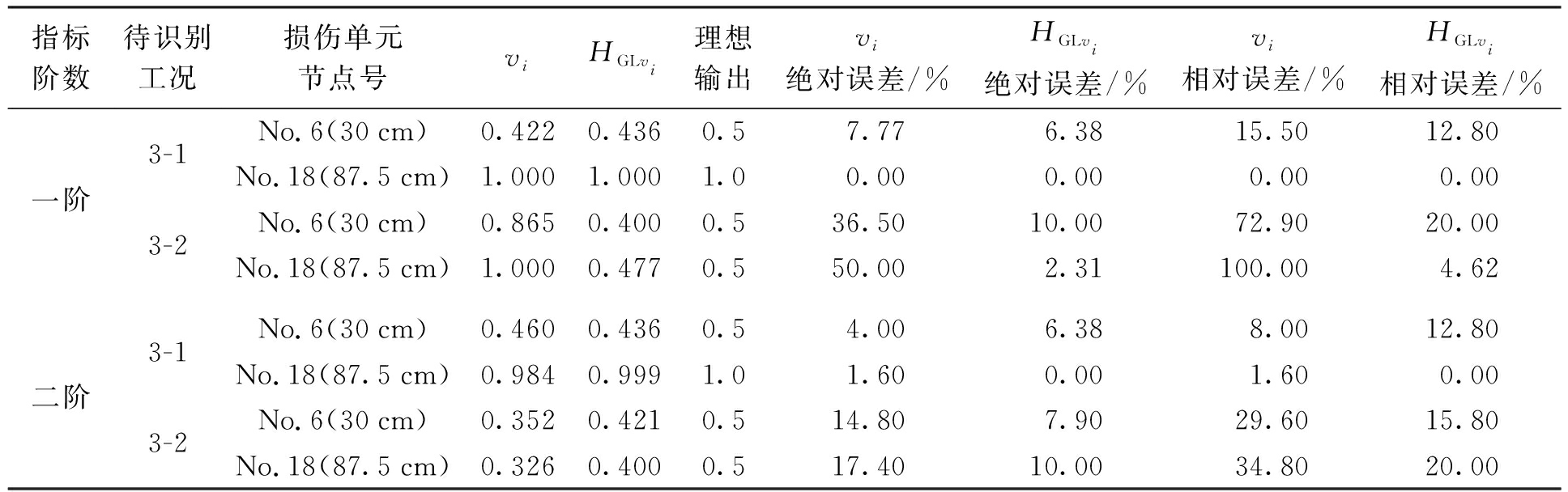
表4 简支钢梁损伤定量识别结果
Tab.4 Quantitative damage identification results of simply supported beam
指标阶数待识别工况损伤单元节点号viHGLvi理想输出vi绝对误差/%HGLvi绝对误差/%vi相对误差/%HGLvi相对误差/%一阶二阶3-13-23-13-2No.6(30cm)0.4220.4360.57.776.3815.5012.80No.18(87.5cm)1.0001.0001.00.000.000.000.00No.6(30cm)0.8650.4000.536.5010.0072.9020.00No.18(87.5cm)1.0000.4770.550.002.31100.004.62No.6(30cm)0.4600.4360.54.006.388.0012.80No.18(87.5cm)0.9840.9991.01.600.001.600.00No.6(30cm)0.3520.4210.514.807.9029.6015.80No.18(87.5cm)0.3260.4000.517.4010.0034.8020.00
对比前两阶指标可知,一、二阶曲率模态指标在各自阶振型节点处的损伤定量识别精度均低于广义局部曲率模态信息熵,靠近一阶振型节点即30 cm处,定量误差达到72.90%,靠近二阶振型节点即87.5 cm处,曲率模态误差达到34.80%,均高于本文提出指标.对于两种损伤工况,指标各自阶振型节点处精度均低于远离振型节点处的损伤识别,这对前文结论进行了验证.
4 结 论
简支梁数值算例中,本文提出的广义局部曲率模态信息熵能够较好进行损伤定位.结合BP神经网络定量损伤时,对比曲率模态,广义局部曲率模态信息熵在判别位置靠近各阶振型节点的损伤时,具有更高的精度.曲率模态在远离振型节点处识别精度较高,两指标互补.本文提出的指标具有无需密集测点即可得到效果良好损伤识别结果的优势.相比其他位置,指标在识别振型节点附近损伤时,对测点数量的改变较为敏感.
通过设置不同位置的参考点对钢梁前两阶振型进行了模态测试.限于试验仪器精度及测试环境影响,本文所提指标结合BP神经网络能够进行大致损伤定量,且在振型节点处指标识别精度优于曲率模态,验证了指标在实际结构中的实用性.
在实际工程中,若损伤位置可测,可通过实际损伤位置,依据曲率模态和广义局部曲率模态信息熵的互补特性选定采用的结构模态采集阶数和损伤指标.本文提出的指标不需要结构的初始模态即可进行损伤识别,加之工程结构中难以获得精度较高的高阶模态振型,使本文提出的方法更具有实际工程意义.
[1] Watt S J,Politi A.Permutation entropy revisited [J].Chaos,Solitons and Fractals,2019,120:95-99.
[2] Sousa Tomé E,Pimentel M,Figueiras J.Damage detection under environmental and operational effects using cointegration analysis:application to experimental data from a cable-stayed bridge [J].Mechanical Systems and Signal Processing,2020,135:1-14.
[3] Wang S Q,Xu M Q,Xia Z P,et al.A novel Tikhonov regularization-based iterative method for structural damage identification of offshore platforms [J].Journal of Marine Science and Technology,2019,24(2):575-592.
[4] 宋福春,刘鉴霆,谢利斌,等.灰色关联度在预应力连续梁桥运营监控中的应用 [J].沈阳工业大学学报,2019,41(6):693-698.
(SONG Fu-chun,LIU Jian-ting,XIE Li-bin,et al.Appli-cation of grey correlation in operation monitoring of prestressed continuous beam bridge [J].Journal of Shenyang University of Technology,2019,41(6):693-698.)
[5] Ghasemi M R,Nobahari M,Shabakhty N.Enhanced optimization-based structural damage detection method using modal strain energy and modal frequencies [J].Engineering with Computers,2018,34(3):637-647.
[6] 刘才玮,苗吉军,高天予,等.基于动力测试的钢筋混凝土梁火灾损伤识别方法 [J].振动与冲击,2019,38(11):121-131.
(LIU Cai-wei,MIAO Ji-jun,GAO Tian-yu,et al.Identification method for fire damage of RC beams based on dynamic tests [J].Journal of Vibration and Shock,2019,38(11):121-131.)
[7] 李雪松,马宏伟,林逸洲.基于卷积神经网络的结构损伤识别 [J].振动与冲击,2019,38(1):159-167.
(LI Xue-song,MA Hong-wei,LIN Yi-zhou.Structural damage identification based on convolution neural network [J].Journal of Vibration and Shock,2019,38(1):159-167.)
[8] Paral A,Singha R D K,Samanta A K.Application of a mode shape derivative-based damage index in artificial neural network for structural damage identification in shear frame building [J].Journal of Civil Structural Health Monitoring,2019,9(3):411-423.
[9] Li H,Bao Y Q,Ou J P.Structural damage identification based on integration of information fusion and Shannon entropy [J].Mechanical Systems and Signal Processing,2008,22(6):1427-1440.
[10] 程建曙.基于信息熵的混凝土桥梁裂缝演化与识别研究 [D].兰州:兰州理工大学,2016.
(CHENG Jian-shu.Research on cracking developing and identification of concrete bridge based on information entropy [D].Lanzhou:Lanzhou University of Technology,2016.)
[11] 丛培江,顾冲时,王建.熵理论在分析混凝土裂缝扩展过程中的应用探讨 [J].应用基础与工程科学学报,2008,16(1):50-56.
(CONG Pei-jiang,GU Chong-shi,WANG Jian.Appli-cation of entropy theory in the analysis of concrete crack propagation process [J].Journal of Basic Science and Engineering,2008,16(1):50-56.)
[12] Yang Z B,Chen X F,Jiang Y Y,et al.Generalised local entropy analysis for crack detection in beam-like structures [J].Nondestructive Testing and Evaluation,2014,29(2):133-153.
[13] 项长生,张亮,高虹,等.广义局部信息熵在混凝土简支梁损伤识别中的应用 [J].兰州理工大学学报,2019,45(4):145-150.
(XIANG Chang-sheng,ZHANG Liang,GAO Hong,et al.Application of generalized local entropy to da-mage detection of simple-supported concrete beam [J].Journal of Lanzhou University of Technology,2019,45(4):145-150.)
[14] 王嵘冰,徐红艳,李波,等.BP神经网络隐含层节点数确定方法研究 [J].计算机技术与发展,2018,28(4):31-35.
(WANG Rong-bing,XU Hong-yan,LI Bo,et al.Research on method of determining hidden layer nodes in BP neural network [J].Computer Technology and Development,2018,28(4):31-35.)