橡胶混凝土作为一种新型的绿色建材,具有自重轻、变形能力强等优势,有较好的抗裂性和抗冲击性,尤其在抗渗和抗冻等耐久性方面具有良好的性能[1-3].为了将这种混凝土更好地在我国季节性冰冻地区推广使用,很有必要对其冻融破坏性能和抗冻性进行预测研究.有关普通混凝土抗冻性的预测,很多学者建立了以经典理论为基础的理论模型和以试验数据做支撑的经验模型,但目前学术界对以上模型均未完全达成共识[4].一般认为,混凝土抗冻性是一个受多因素影响的复杂性和争议性问题,涉及到许多不确定的影响因素,建立理论模型要用到材料学、力学、化学等多个学科的理论知识,还要结合亚微观和宏观两个层面来研究,就目前来说,建立理论模型的难度相当大.而目前的经验模型多以冻融机理为宏观指导,考虑影响混凝土抗冻性的主要因素,以试验数据为基础进行回归分析,建立经验模型,但模型的实用性有待商榷[5].相对于普通水泥混凝土而言,橡胶混凝土中由于掺入了橡胶粉,混凝土的各种性质都发生了不同程度的改变,使其抗冻耐久性问题也变得更为复杂,建立理论模型的难度就更大[6].人工神经网络模型由于强大的非线性映射能力和自适应学习、记忆的特点,使其非常适合解决混凝土抗碳化性能、抗化学侵蚀性能和抗冻性预测等一系列耐久性问题[7-8],因此,本文将运用人工神经网络对橡胶混凝土的抗冻性进行分析.为获得足够数量的训练样本和测试样本进行了橡胶混凝土的冻融试验,以相对动弹性模量作为衡量抗冻性的重要指标.选用MATLAB神经网络工具箱中的BP网络模型,以试验所得数据为基础,建立橡胶混凝土的相对动弹性模量BP网络预测模型,对其抗冻性进行预测,为工程应用提供参考.
1 橡胶混凝土冻融试验
1.1 试验原材料
本次冻融试验采用的橡胶集料为沈阳天禹橡胶粉厂生产的50目橡胶粉,表观密度为1 020 kg/m3.所用水泥为沈阳产PO42.5级普通硅酸盐水泥.细骨料采用普通河砂,细度模数为2.55,表观密度为2 600 kg/m3.粗骨料采用最大粒径为25 mm的碎石,进行5~25 mm连续级配,表观密度为2 650 kg/m3.
1.2 试验配合比
在橡胶混凝土抗冻性试验中,配合比设计采用正交试验设计方法.以C40级普通混凝土的配合比为基础,运用常规配合比设计方法确定每立方米混凝土中各组成材料的质量,然后分别用不同掺量粒径为50目的橡胶粉等体积替换细骨料砂.采用橡胶掺量WR、水灰比W/B和砂率Sp 3个重要因素的4个水平进行设计,共得到16组不同配合比试件.橡胶掺量WR取5%、10%、15%和20%,分别用A1、A2、A3和A4来表示;水灰比W/B取0.35、0.40、0.45和0.50,分别用B1、B2、B3和B4来表示;砂率Sp取0.33、0.34、0.35和0.36,分别用C1、C2、C3和C4来表示.具体的配合比信息详见文献[6].
1.3 试验方法
试验采用《普通混凝土长期性能和耐久性能试验方法标准》(GB/T50082-2009)中的快冻法[9],试件尺寸为100 mm×100 mm×400 mm.通常来说,动弹性模量对混凝土结构在冻融循环作用下的内部损伤尤为敏感,而且可以运用动弹仪进行无损检测来测定,可减少大量的试验工作量,节约试验试件和成本[10].因此,该试验中以相对动弹性模量作为分析和评价橡胶混凝土抗冻性能的重要参数.图1为运用动弹仪对冻融循环每隔25次的试件进行动弹性模量的测定.

图1 冻融循环试验后测定试件的动弹性模量
Fig.1 Dynamic elasticity modulus of samples after freeze-thaw cycle tests
1.4 试验结果
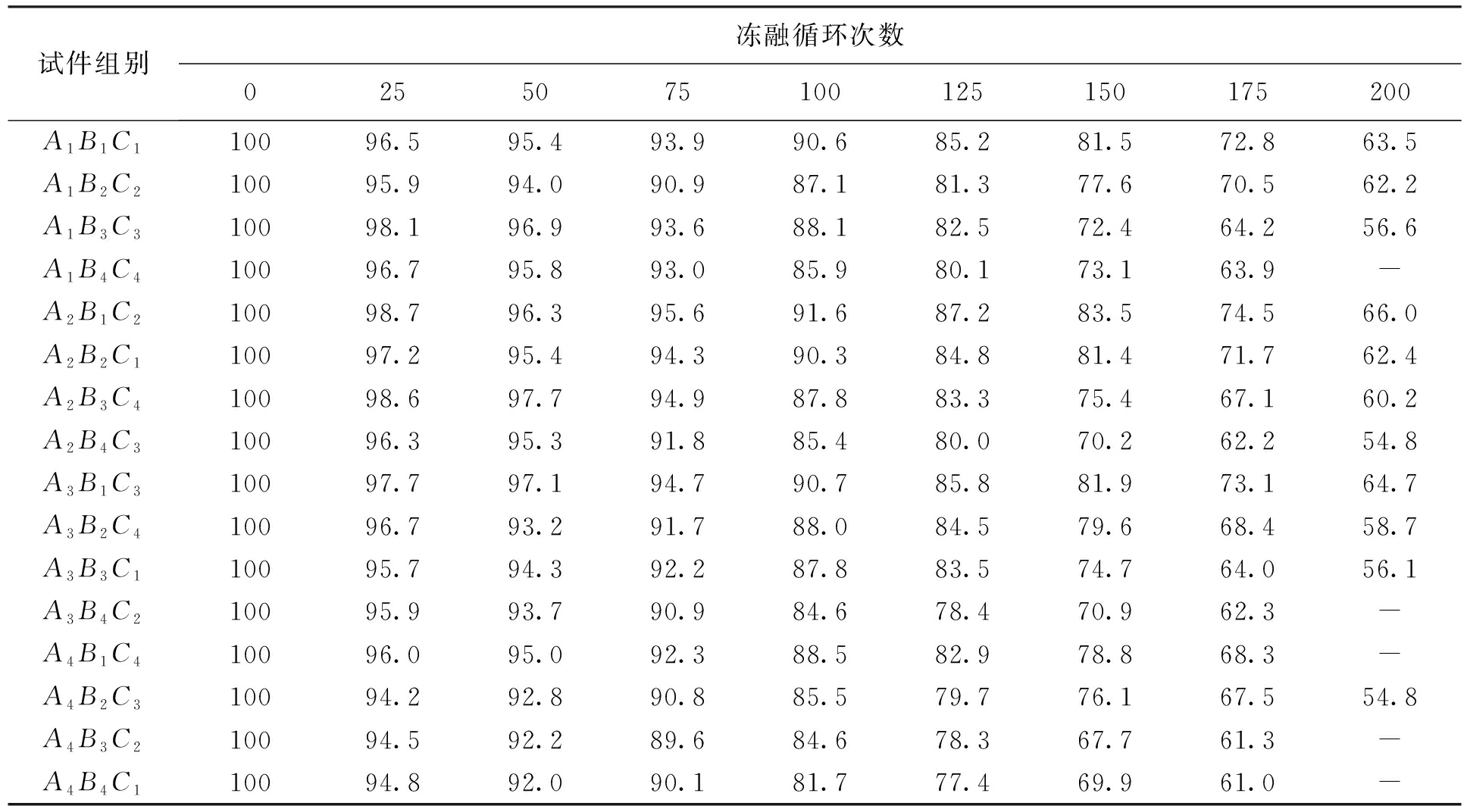
经过不同冻融循环次数后,按照上述试验方法测定并计算得到各组橡胶混凝土试件的相对动弹性模量,如表1所示.通过对上述试验结果进行极差分析和方差分析可知,在选取的橡胶掺量WR、水灰比W/B和砂率Sp这三个试验因素中,橡胶掺量和水灰比对动弹性模量影响显著,砂率的影响很小.
表1 冻融循环作用下橡胶粉混凝土相对动弹性模量
Tab.1 Relative dynamic elasticity modulus of rubber powder concrete subjected to freeze-thaw cycles %
试件组别冻融循环次数0255075100125150175200A1B1C110096.595.493.990.685.281.572.863.5A1B2C210095.994.090.987.181.377.670.562.2A1B3C310098.196.993.688.182.572.464.256.6A1B4C410096.795.893.085.980.173.163.9-A2B1C210098.796.395.691.687.283.574.566.0A2B2C110097.295.494.390.384.881.471.762.4A2B3C410098.697.794.987.883.375.467.160.2A2B4C310096.395.391.885.480.070.262.254.8A3B1C310097.797.194.790.785.881.973.164.7A3B2C410096.793.291.788.084.579.668.458.7A3B3C110095.794.392.287.883.574.764.056.1A3B4C210095.993.790.984.678.470.962.3-A4B1C410096.095.092.388.582.978.868.3-A4B2C310094.292.890.885.579.776.167.554.8A4B3C210094.592.289.684.678.367.761.3-A4B4C110094.892.090.181.777.469.961.0-
2 橡胶混凝土样本
2.1 样本的收集和分类
以冻融试验获得的掺入50目橡胶粉的混凝土相对动弹性模量试验数据为研究依据,考虑不同橡胶掺量、水灰比和冻融循环次数等因素变化带来的影响,对其相对动弹性模量进行分析和预测,共收集到139组试验数据.将这些数据组进行随机排列,得到整个数据样本集.确定前112组作为网络模型的训练样本(约占整个数据样本的80%),后27组作为网络模型的测试样本(约占整个数据样本的20%).考虑到各组试件采用的砂率均在合理范围内,且其变化对各组试件的动弹性模量影响不显著,所以忽略砂率这一次要因素,确定BP网络的输入参数分别为橡胶掺量x1、水灰比x2和冻融循环次数x3,输出参数为相对动弹性模量y.各参数取值为:橡胶掺量x1为5%、10%、15%和20%;水灰比x2为0.35、0.40、0.45和0.50;冻融循环次数x3为0、25、50、…、200;相对动弹性模量y为50%~100%.
2.2 样本数据的归一化
由于冻融循环次数和相对动弹性模量分布范围较大,为了避免因某个净输入绝对值过大而使BP神经元输出饱和,使权值调整进入平坦区,也为了避免某些数值很小但却对输出影响较大的向量被忽略,导致因输入参数不均匀而引起的输出失真和网络麻痹现象,需要对原始数据进行尺度变换处理,即数据的归一化处理.本文采用式(1)对输入变量x3和输出变量y进行归一化处理,将输入及输出参数变换在[0.2,0.8]的区间内,即
(1)
式中:m′为归一化处理后的值;m为原始数据真实值;mmin、mmax为原始数据真实值中的最小值和最大值.
3 相对动弹性模量BP网络模型
3.1 模型建立
运用MATLAB神经网络工具箱中的BP网络模型,设置网络模型参数如下:
1) 输入层.输入节点数为3,即橡胶掺量x1、水灰比x2和冻融循环次数x3.
2) 输出层.输出节点数为1,即相对动弹性模量y.
3) 训练允许误差.均方差MSE=0.000 1.
4) 隐含层.隐含层为1层,隐含层节点数为18,是通过反复试算后确定的.
5) 传递函数.确定输入层与隐含层之间、隐含层与输出层之间的传递函数均为Tansig.
6) 训练函数.采用Trainlm.BP网络的训练函数包括:梯度下降BP算法训练函数Traingd、动量反传递的梯度下降BP算法训练函数Traingdm、动态自适应学习率的梯度下降BP算法训练函数Traingda、动量反传递和动态自适应学习率的梯度下降BP算法训练函数Traingdx与Levenberg-marquardt的BP算法训练函数Trainlm.本文采用Trainlm是因为该函数通过自适应调整可以获取最快的调整量,收敛速度较快.
7) 学习函数.采用带动量项的Learngdm.
橡胶混凝土相对动弹性模量的BP网络结构如图2所示.
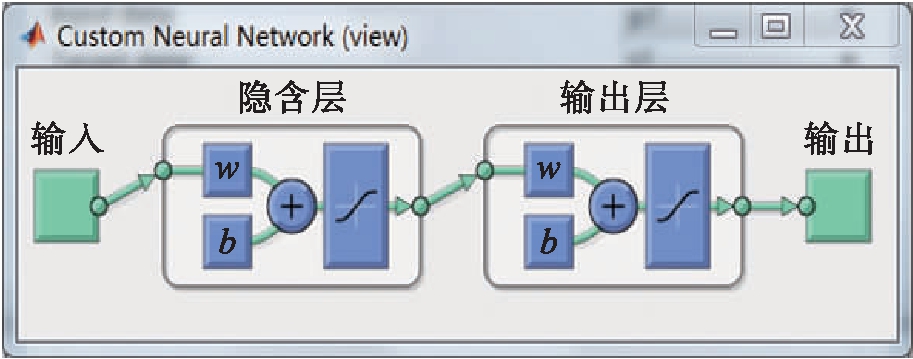
图2 橡胶混凝土相对动弹性模量的BP网络结构
Fig.2 BP network structure of relative dynamic elasticity modulus of rubber concrete
3.2 模型训练
运用图2中的BP网络模型,训练结束后得到的训练误差为7.12e-05,达到了预定的MSE=0.000 1的精度要求.将该模型训练结果与训练样本实测结果进行对比,结果如图3所示.由图3可知,该网络模型的训练结果与实测结果比较吻合.
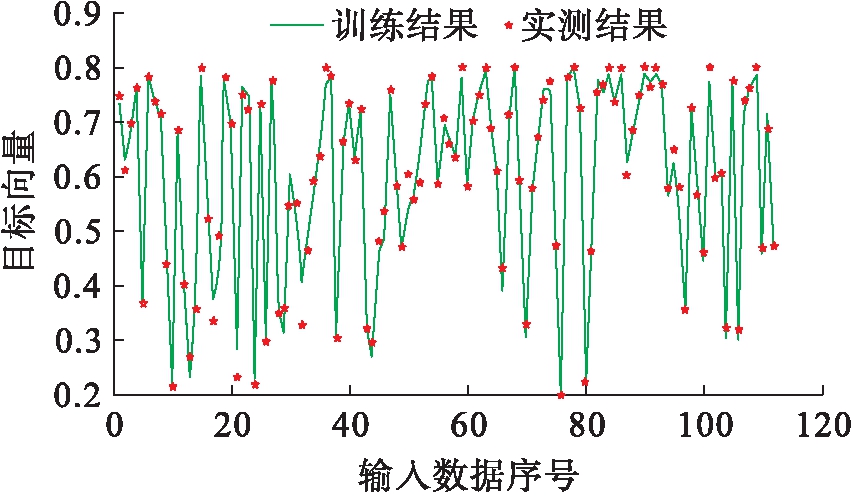
图3 相对动弹性模量训练结果和实测结果对比
Fig.3 Comparison between trained and measured results for relative dynamic elasticity modulus
该橡胶混凝土相对动弹性模量BP网络的权值和阈值分别为


b2=[-1.034 6]
3.3 模型测试
运用该模型对27组橡胶混凝土相对动弹性模量预测样本进行测试,其预测结果如图4所示.预测结果和实测值的变化趋势基本一致,但两者之间存在一定的误差,为了更清晰地了解该网络模型的性能,将预测结果反归一化处理,其表达式为
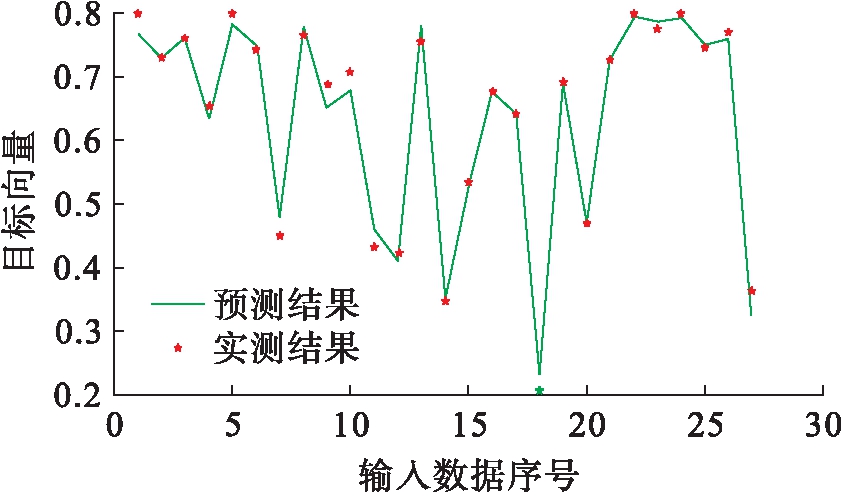
图4 相对动弹性模量预测结果和实测结果对比
Fig.4 Comparison between predicted and measured results for relative dynamic elasticity modulus
(2)
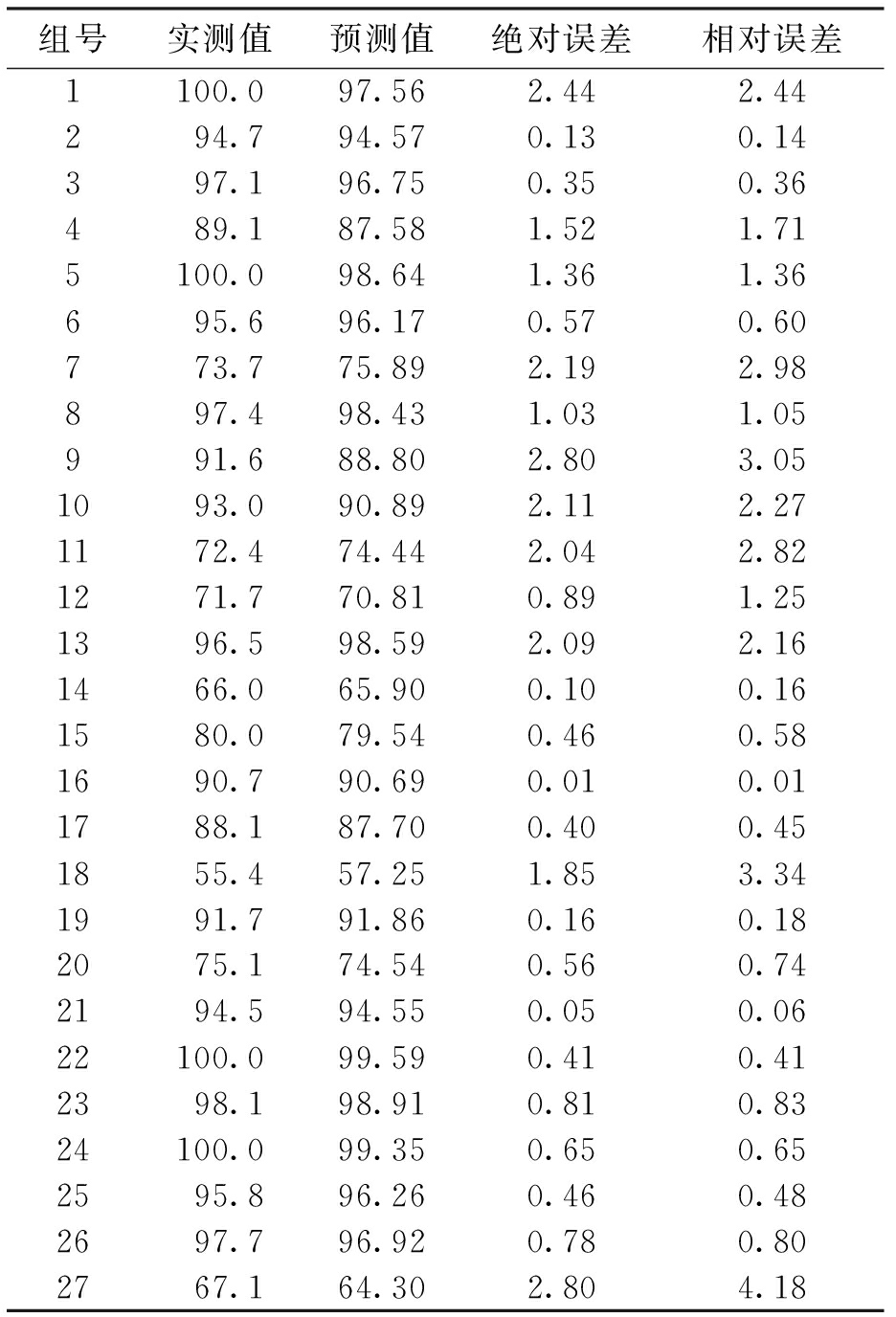
由式(2)可得各组橡胶混凝土试件的相对动弹性模量预测值.将预测值与实测值进行对比,其绝对误差和相对误差如表2所示.
表2 相对动弹性模量的BP网络预测值和误差
Tab.2 Predicted values and errors of relative dynamic elasticity modulus %
组号实测值预测值绝对误差相对误差1100.097.562.442.44294.794.570.130.14397.196.750.350.36489.187.581.521.715100.098.641.361.36695.696.170.570.60773.775.892.192.98897.498.431.031.05991.688.802.803.051093.090.892.112.271172.474.442.042.821271.770.810.891.251396.598.592.092.161466.065.900.100.161580.079.540.460.581690.790.690.010.011788.187.700.400.451855.457.251.853.341991.791.860.160.182075.174.540.560.742194.594.550.050.0622100.099.590.410.412398.198.910.810.8324100.099.350.650.652595.896.260.460.482697.796.920.780.802767.164.302.804.18
由表2中橡胶混凝土相对动弹性模量的预测结果可以看出,大部分测试样本的误差都较小,有88.9%的测试样本相对误差均低于3%,只有11.1%的测试样本相对误差超过了3%,但均未超过5%,能够满足实际工程的精度要求.因此,运用该BP网络模型可以较好地对冻融循环作用下橡胶粉混凝土的相对动弹性模量进行预测.
4 结 论
本文通过分析得出以下结论:
1) 橡胶混凝土在冻融循环作用下的抗冻性受多种因素影响,本文所建立的橡胶混凝土抗冻性BP网络模型,以橡胶掺量、水灰比和冻融循环次数为输入变量,以相对动弹性模量为输出变量,避免了建立精确的数学理论模型所面临的困境.
2) 该BP网络模型输入层与隐含层之间、隐含层与输出层之间的传递函数均为Tansig,训练函数为Trainlm,学习函数为Learngdm.模型收敛速度非常快,训练结束后得到的训练误差为7.12e-05.
3) 经测试样本验证,该BP网络模型具有较强的预测能力,其预测结果与试验结果吻合较好,精度较高,88.9%的测试样本相对误差均低于3%,所有测试样本的相对误差均未超过5%.随着训练样本数量的增加,通过超强的自我学习能力,预测能力和精度将进一步提高.能够满足实际工程的精度要求,可用于橡胶混凝土工程的抗冻性评估和预测.
[1] 何亮,黄勇,冯畅,等.橡胶混凝土性能及胶粉表面改性研究进展 [J].硅酸盐通报,2018,37(8):2483-2489.
(HE Liang,HUANG Yong,FENG Chang,et al.Research progress on properties of rubberized concrete and the surface modification of crumb rubber [J].Bulletin of the Chinese Ceramic Society,2018,37(8):2483-2489.)
[2] 刘松岸,刘亚飞.改性处理对橡胶混凝土力学性能及耐久性影响研究 [J].混凝土,2018(7):34-36.
(LIU Song-an,LIU Ya-fei.Effects of modification of rubber particles on mechanical property and durability rubberized concrete [J].Concrete,2018(7):34-36.)
[3] 张克.改性橡胶再生粗骨料混凝土力学性能及抗冻性能的试验研究 [D].呼和浩特:内蒙古农业大学,2018.
(ZHANG Ke.Experimental research on mechanical properties and frost resistance of modified rubber recycled concrete [D].Hohhot:Inner Mongolia Agricultural University,2018.)
[4] 肖前慧,牛荻涛.冻融和碳化共同作用下混凝土损伤分析 [J].建筑材料学报,2015,18(5):763-766.
(XIAO Qian-hui,NIU Di-tao.Damage model for concrete subjected to freeze-thaw cycles and carbonation [J].Journal of Building Materials,2015,18(5):763-766.)
[5] 龙广成,刘赫,马昆林,等.考虑冻融作用的混凝土单轴压缩损伤本构模型 [J].中南大学学报(自然科学版),2018,49(8):1884-1892.
(LONG Guang-cheng,LIU He,MA Kun-lin,et al.Uniaxial compression damage constitutive model of concrete subjected to freezing and thawing [J].Journal of Central South University (Science and Technology),2018,49(8):1884-1892.)
[6] 徐金花.考虑环境作用的橡胶集料混凝土力学性能及耐久性研究 [D].沈阳:东北大学,2016.
(XU Jin-hua.Research on mechanical behaviors and durability of rubber concrete under environmental conditions [D].Shenyang:Northeastern University,2016.)
[7] 陈晓雨,孔丽娟,刘行,等.基于神经网络预测粗骨料对混凝土抗碳化性能的影响 [J].工业建筑,2016,46(增刊):618-622.
(CHEN Xiao-yu,KONG Li-juan,LIU Xing,et al.Prediction of carbonization resistance of concrete with different coarse aggregates using BP artificial neural network [J].Industrial Construction,2016,46(Sup):618-622.)
[8] 李扬,王伯昕,陈冬昕,等.基于BP神经网络预测复合盐侵蚀后混凝土的相对动弹性模量 [J].混凝土,2018(7):21-23.
(LI Yang,WANG Bo-xin,CHEN Dong-xin,et al.Prediction of relative dynamic elastic modulus of concrete after erosion based on BP neutral network theory [J].Concrete,2018(7):21-23.)
[9] 中华人民共和国住房和城乡建设部.GB/T50082-2009普通混凝土长期性能和耐久性能试验方法标准 [S].北京:中国建筑工业出版社,2009.
(Ministry of Housing and Urban-Rural Development of the People’s Republic of China.GB/T50082-2009 Standard for test methods of long-term performance and durability of ordinary concrete [S].Beijing:China Construction Industry Press,2009.)
[10] 王海军,高勇,魏华,等.混凝土在压应力状态下的抗冻性试验分析 [J].沈阳工业大学学报,2016,38(4):445-449.
(WANG Hai-jun,GAO Yong,WEI Hua,et al.Expe-rimental analysis on frost resistance property of concrete at compressive stress state [J].Journal of Shenyang University of Technology,2016,38(4):445-449.)