玉米作为我国主要农作物之一,不仅可以满足人民的口粮需要,同时也是养殖业的主要饲料来源。近年来,玉米在工业原料以及生物能源原料中发挥着重要作用。然而由于国内玉米临储政策,玉米库存大量积压,市场价格“扭曲”。2016年,在供给侧改革的背景下,政府为了促进玉米市场健康、可持续发展,取消了临储政策,形成了玉米价格以市场定价为原则另加政府补贴的新价格机制。玉米市场的这一系列改革可以达到去产能、去库存的效果,优化了我国的粮食生产结构,但对玉米的价格波动造成了很大的影响。玉米价格的大幅度波动会对国民经济的相关行业以及农民的生活产生较大影响。本文通过X12季节调整法和H-P滤波法将玉米价格进行分解,分析其波动趋势,并利用ARIMA模型预测玉米短期内的价格走势。
一、研究现状
农产品价格走势是国内外学者的研究重点。Moore曾在《棉花产量与价格预测》一书中,选择降雨量和温度两个指标作为自变量建立了回归模型,并对棉花的产量和价格进行了预测[1]。自此,经济学家对计量经济学模型的研究开始兴起,包括一元回归模型、多元回归模型、平滑指数模型等,其中在1925年Sarle利用38年的猪肉价格数据作为样本,建立了拟合度高达75%的猪肉价格预测模型[2],是价格预测史上的主要成就之一。近年来,随着越来越多计量模型的提出,对农产品价格的分析预测研究十分常见。Chen等采用资产定价模型对农产品价格进行预测,结果表明货币市场和和期权市场的信息可以用来预测国际农产品价格[3]。Talawar运用广义自回归条件异方差模型对印度南部卡纳塔克邦不同市场的玉米价格进行预测,结果表明此模型可以很好地拟合实际价格[4]。Jha和Sinha分别利用ARIMA模型和时延神经网络回归模型对大豆和油菜籽的月度数据进行价格预测,结果表明时延神经网络回归模型的预测准确度要优于ARIMA模型[5]。
国内也有很多学者将各经济模型运用到时间序列的建模分析和价格预测上。余洁等曾经运用X12模型、H-P滤波法分析了生鲜奶的价格波动趋势,并基于此预测了未来两年生鲜奶的价格走势[6]。李哲敏和李干琼选取了禽蛋市场价格的影响因子,通过建立多元回归预测模型对禽蛋的短期价格进行了预测[7]。李敏等在分析香菇价格波动规律后,对其月度价格建立了ARIMA模型,并验证了该模型可以很好地拟合香菇的月度价格[8]。王素雅分别对北京新发地市苹果价格的日、周、月度数据建立了GARCH模型、ARIMA模型以及VAR模型,结果表明GARCH模型对日数据的预测精准度最高,ARIMA模型对周数据和月度数据的预测精准度最高[9]。李正辉等利用小波分析法对我国农产品价格指数进行分析,解释了波动原因[10]。陈灿煌通过价格分解对我国农产品价格指数进行分解,结果表明我国农产品价格指数的最大影响因素就是季节性和随机性[11]。
二、玉米价格波动分析
1. 模型概述
X12季节调整模型是美国商务部人口普查局提出的季节调整方法,是对X11模型的优化和补充[12]。该模型通过将时间序列分解为对应的长期趋势循环分量序列、季节周期分量序列和随机分量序列,来减少因各变量之间的相互干扰带来的研究误差。X12季节调整模型包括乘法模型、加法模型、伪加法模型和对数加法模型,较为典型的有两种:加法模型一般形式为Yt=TCt+St+It,乘法模型一般形式为Yt=TCtStIt。式中:Yt为时间要素;TCt为趋势循环要素;St为季节要素;It为随机要素[13]。
H-P滤波法由Hodrick和Prescott在分析战后美国经济周期时首次提出。他们认为时间序列在经过X12季节调整后循环周期成分和趋势成分仍然是叠加在一起的,而H-P滤波法可以将二者进一步分离。假设一个时间序列只含有趋势成分![]() 和周期成分
和周期成分![]() 则
则![]() 滤波法就是在分离出
滤波法就是在分离出![]() 后,使得
后,使得![]() 最小化,λ为惩罚因子,一般使用月度数据时,λ为14 400[14]。
最小化,λ为惩罚因子,一般使用月度数据时,λ为14 400[14]。
2. 数据分析
由于季节调整模型要求数据必须为月度数据或季度数据[15],为了保证分析结果的准确性和时效性,本文选取2007年1月—2018年3月的全国玉米平均价的月度数据作为研究数据,共135组观测值。数据来源于中国畜牧业信息网(http://www.caaa.cn),具体如表1、图1所示。
表1 玉米月度价格 元/千克
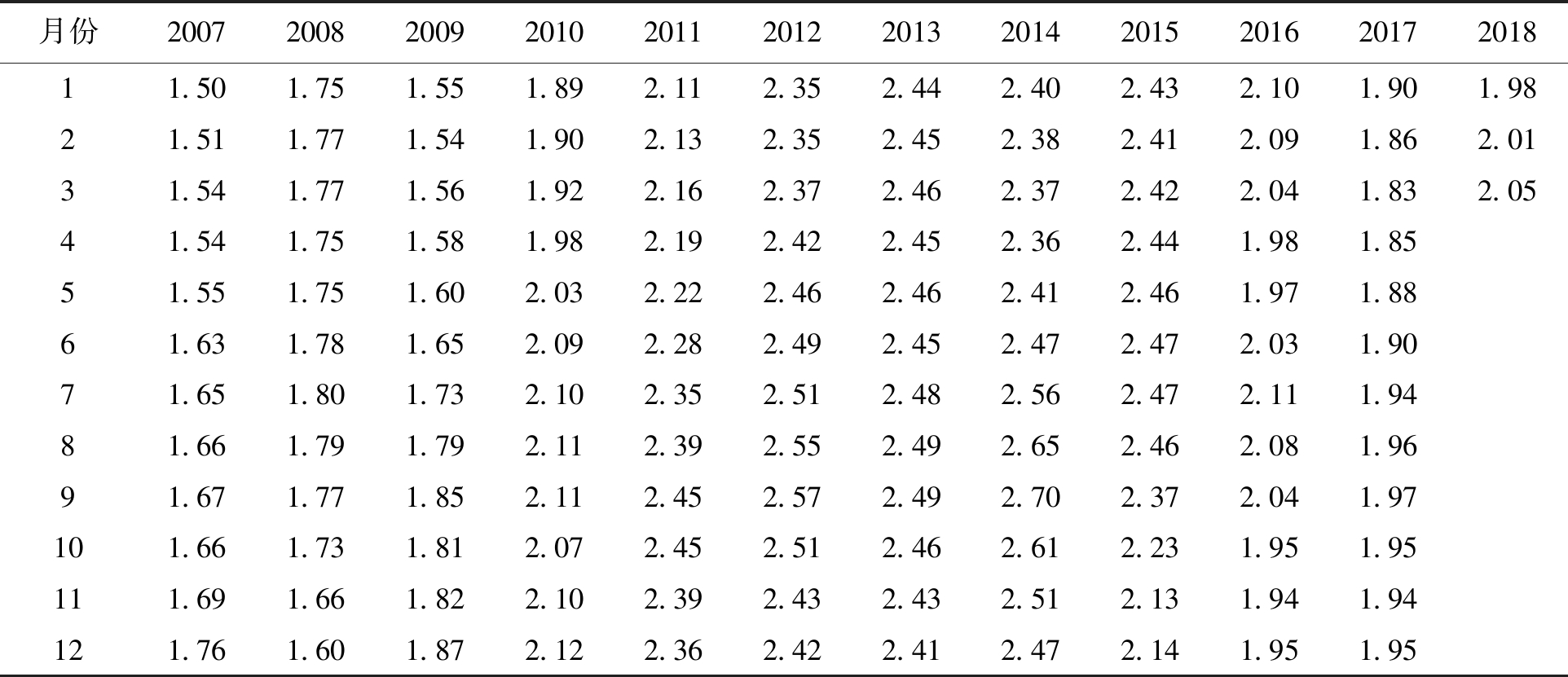
月份20072008200920102011201220132014201520162017201811.501.751.551.892.112.352.442.402.432.101.901.9821.511.771.541.902.132.352.452.382.412.091.862.0131.541.771.561.922.162.372.462.372.422.041.832.0541.541.751.581.982.192.422.452.362.441.981.8551.551.751.602.032.222.462.462.412.461.971.8861.631.781.652.092.282.492.452.472.472.031.9071.651.801.732.102.352.512.482.562.472.111.9481.661.791.792.112.392.552.492.652.462.081.9691.671.771.852.112.452.572.492.702.372.041.97101.661.731.812.072.452.512.462.612.231.951.95111.691.661.822.102.392.432.432.512.131.941.94121.761.601.872.122.362.422.412.472.141.951.95
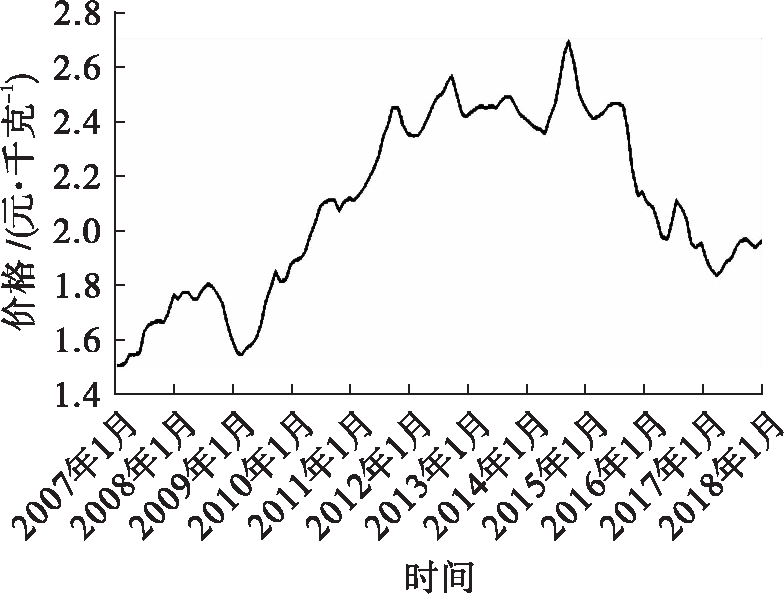
图1 玉米月度价格走势
由表1、图1可知,我国近十年玉米价格总体呈现先上升后下降的趋势,并且短期的波动较为明显。玉米价格从2007年1月到2018年3月大致可以分为三个周期:从2007年1月开始,玉米价格呈现出阶梯式上升的趋势,到2008年7月为样本周期的阶段性高点,月平均价格为1.80元/千克,之后开始直线下降,一直到2009年2月达到波谷1.54元/千克,此为第一个波动周期,周期内的平均价格为1.67元/千克,振幅为16.9%。第二个周期是2009年3月—2017年3月,时间跨度较长,虽然周期内有较多的短期波动,但是总体上呈现先上升后下降的趋势,波峰为2014年9月,月平均价格为2.70元/千克。第二个周期的平均价格为2.23,振幅为75.3%,与第一个周期相比增长较不稳定。第三个周期从2017年4月开始,玉米价格在经历较长时间的下降后开始出现回升的趋势。
利用X12季节调整法对玉米价格时间序列进行分解,得到四个序列,具体如图2~5所示。由图3可知,玉米价格的季节波动规律明显,波动的幅度和时间跨度基本相似。波峰为每年的7、8月,此时玉米价格受季节影响会有上升的趋势;波谷为每年的1、2月,此时玉米的价格受季节影响会有下降的趋势。玉米价格受季节因素影响较大,这与玉米生长的环境和温度极大相关。图4为玉米价格的随机因素时间序列图,随机因素是一种无规律可循的变动,包括国家的政策调整、洪涝干旱等偶然性因素。
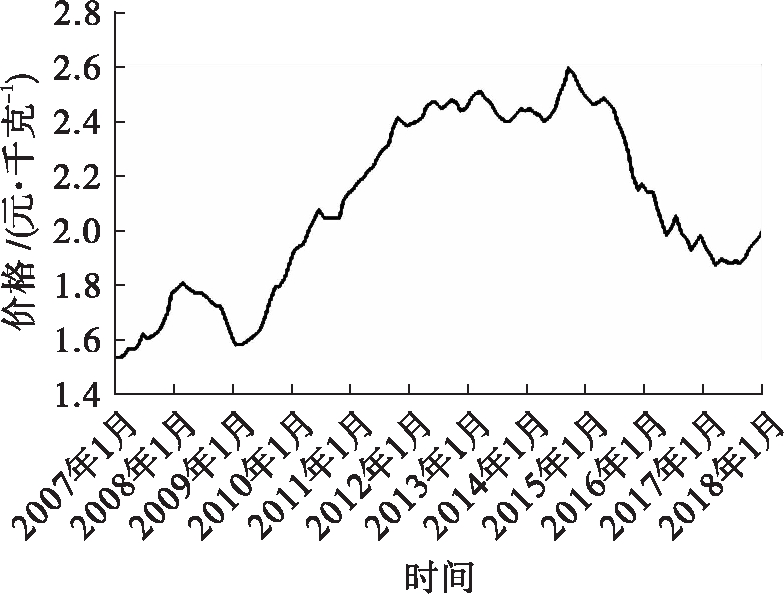
图2 季节调整后的玉米价格
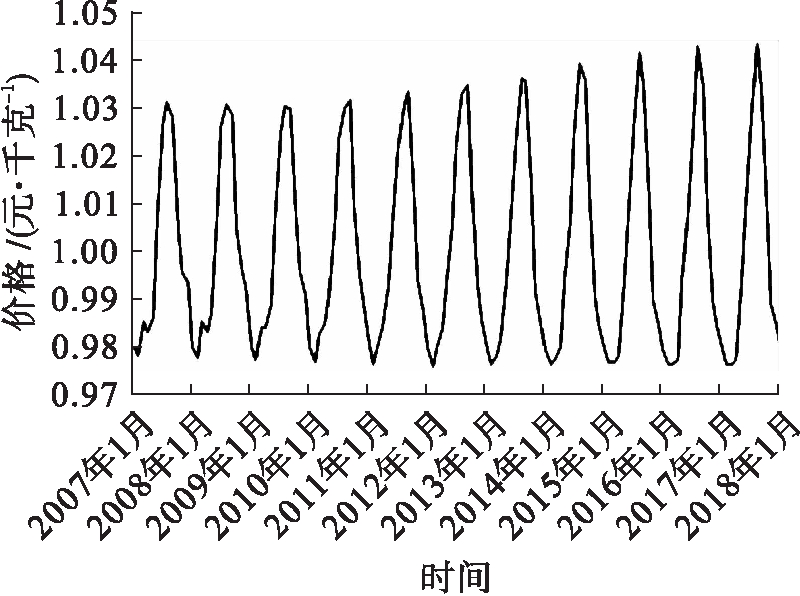
图3 季节因素序列
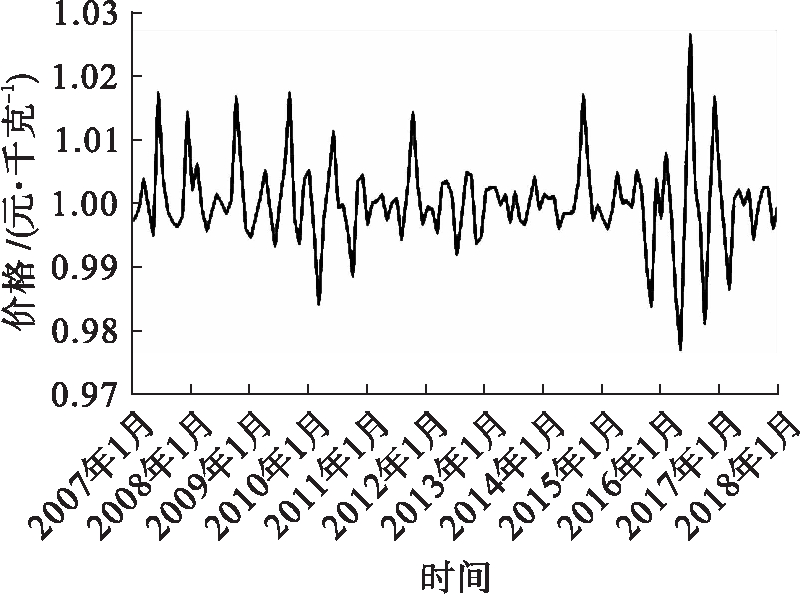
图4 随机因素序列
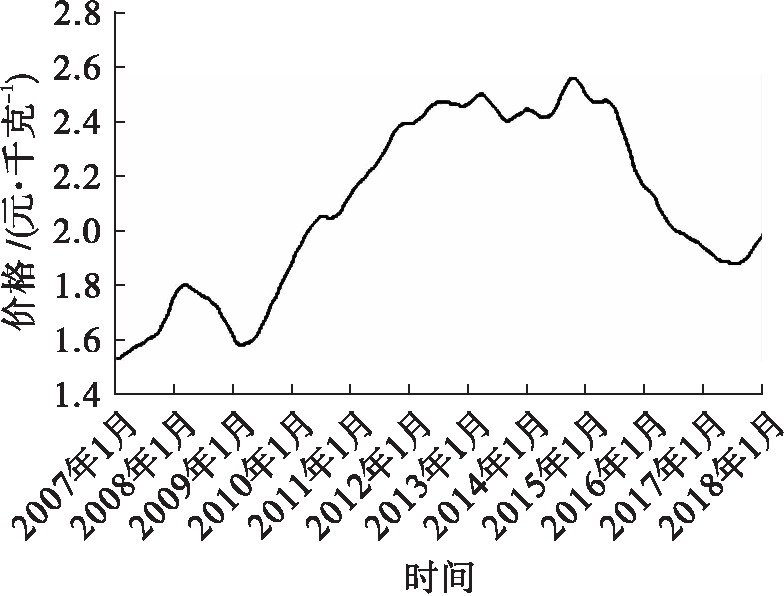
图5 循环趋势序列
利用H-P滤波法将循环趋势序列分解为趋势因素和循环因素,具体如图6所示。由图6可知,从长期趋势曲线看,玉米价格先上升后下降,2007年1月—2013年8月为上升阶段,2013年9月—2018年3月为下降阶段。玉米价格的长期趋势是由玉米的供给和需求决定的。2013年以前,由于人们日常生活对口粮的需要、兴起的养殖业以及国家临储政策,对玉米的需求远远大于玉米的供给,使得玉米价格只升不降;但是随着政策的推进,玉米行业开始出现了库存积压、供大于求的问题。2016年国家取消了玉米临储政策,市场对玉米的需求大幅度下降,价格也下降到2011年以来的新低[16]。
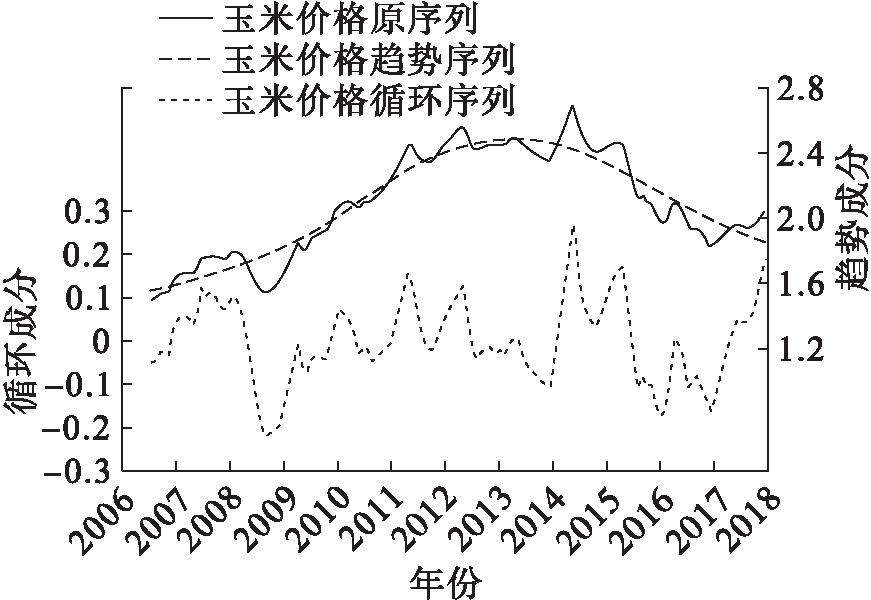
图6 H-P滤波法分解
可见,玉米价格的周期曲线围绕着0值上下波动。将0值以上的部分定义为波峰,将0值以下的部分定义为波谷,可以大致将整个周期曲线分为三个完整的周期,具体如表2所示。由表2可知,玉米价格大约每三年形成一个波动周期,每个周期大约持续40个月。第一个周期为2007年1月—2010年5月。2007年以前玉米市场低迷,价格持续走低,国家在2008年出台玉米临储政策后,玉米价格有了小幅度的回升。第二个周期为2010年6月—2014年6月。在限价的基础上,玉米价格的增长速度比较稳定,波峰到波谷的振幅由235.71%降到200%。2014年7月—2017年10月为第三个周期。2014年玉米价格持续走高,最高达到2.7元/千克,但由于国内玉米供大于求,2014年以后开始出现下降趋势,振幅下降到178.57%,与前两期相比波动更加稳定。另外,在农业供给侧改革的背景下,为了农产品结构优化以及玉米行业稳定健康的发展,政府取消临储政策,将玉米价格交由市场决定,因此玉米价格的波动幅度会越来越趋于稳定。本文预测下一个波动周期大约为2017年11月—2020年12月,并且短期内玉米价格虽不能回升到2014年的水平,但与上年同期相比会有小幅度的上升。
表2 玉米价格周期划分情况

周期波峰时间波谷时间周期长度/月振幅/%2007年1月—2010年5月2008年2月2009年2月41235.712010年6月—2014年6月2011年10月2013年8月48200.002014年7月—2017年10月2014年10月2016年6月40178.572017年11月—2020年12月---
三、玉米价格预测
对玉米的价格序列进行季节调整后,利用ARIMA模型对其进行短期的价格预测。实证数据选取2007年1月—2016年12月年玉米平均价格的月度数据,2017年1月—2018年3月数据作为与预测数据对比的依据。ARIMA模型全称为自回归积分滑动平均模型(autoregressive integrated moving average model),由自回归模型(AR)和移动平均模型(MR)组成,是博克思(Box)和詹金斯(Jenkins)提出的著名时间序列预测方法,所以又称B-J模型[17]。实际建模中,时间序列可能是非平稳的,通过若干次差分将其转化为平稳序列,再将其表示成关于前期值的自回归和关于白噪声的移动平均的组合,记为ARIMA(p,d,q),用数学公式可以表示为ΔdYt=φ1ΔdYt-1+…+φpΔdYt-p+εt+θ1εt-1+…+θqεt-q。式中,ΔdYt为Yt经过d阶差分后平稳的d阶单整序列;φi(i=1,2,…,p)、θk(k=1,2,…,q)为自回归模型和移动平均模型的系数;εt为白噪声序列[18]。
1. 平稳性检验
利用ARIMA模型进行预测时,要求时间序列为平稳序列[19],故进行平稳性检验,结果如表3所示。由图1可知,玉米的价格走势为先上升后下降,初步断定为非平稳序列,然后利用单位根检验法进一步判断其平稳性。在给定的显著性水平下,若单位根的临界值小于T统计量,则时间序列为非平稳序列;若单位根的临界值大于T统计量,则时间序列为平稳序列[20]。由表3可知,玉米价格原序列的T统计量值大于5%临界值,序列非平稳;一阶差分后序列的T统计量值小于5%临界值,序列平稳,因此可以对玉米价格的一阶差分序列建立ARIMA模型。
表3 平稳性检验结果

变量T统计量5%临界值P值原序列-1.713431-2.8860740.4219一阶差分序列-5.488645-2.8860740.0000
2. 模型建立
ARIMA(p,d,q)模型一般采用自相关图法和AIC、SC最小信息准则法确定p、q的值[21]。利用Eviews7.2对一阶差分后的玉米价格序列进行自相关检验,结果显示自相关拖尾、偏自相关一阶截尾,可初步确定p=1,q=0。为了保证模型的最优,取p=1、q=0,1,2,用最小二乘法分别拟合ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(1,1,2)三个模型,结果如表4所示,根据AIC、SC最小信息准则法,ARIMA(1,1,0)的拟合效果最优,可初步建立模型ΔYt=φ1ΔYt-1+εt。
表4 模型定阶判断指标
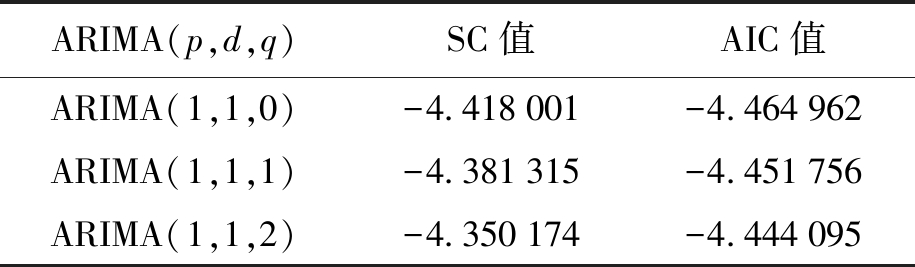
ARIMA(p,d,q)SC值AIC值ARIMA(1,1,0)-4.418001-4.464962ARIMA(1,1,1)-4.381315-4.451756ARIMA(1,1,2)-4.350174-4.444095
为了进一步判断模型的适应性,对模型的残差序列进行白噪声检验。若Q统计量的P值小于0.05,说明模型残差序列存在自相关,信息提取得不够完全,需要重新建模;若P值大于0.05,则模型残差序列通过白噪声检验,模型是适应的[21]。利用Eviews7.2输出ARIMA(1,1,0)模型的残差序列的自相关函数值以及对应的统计量值和P值,具体如表5所示。从第2阶开始到第20阶P值全部大于0.05,说明模型的残差序列为白噪声序列,模型的适应性较好。利用Eviews的Estimate equation功能求得ARIMA(1,1,0)的各项系数为C=0.003 745,AR(1)=0.587 379,则模型的表达式为ΔYt=0.587 379ΔYt-1+0.003 745。
表5 残差白噪声检验结果
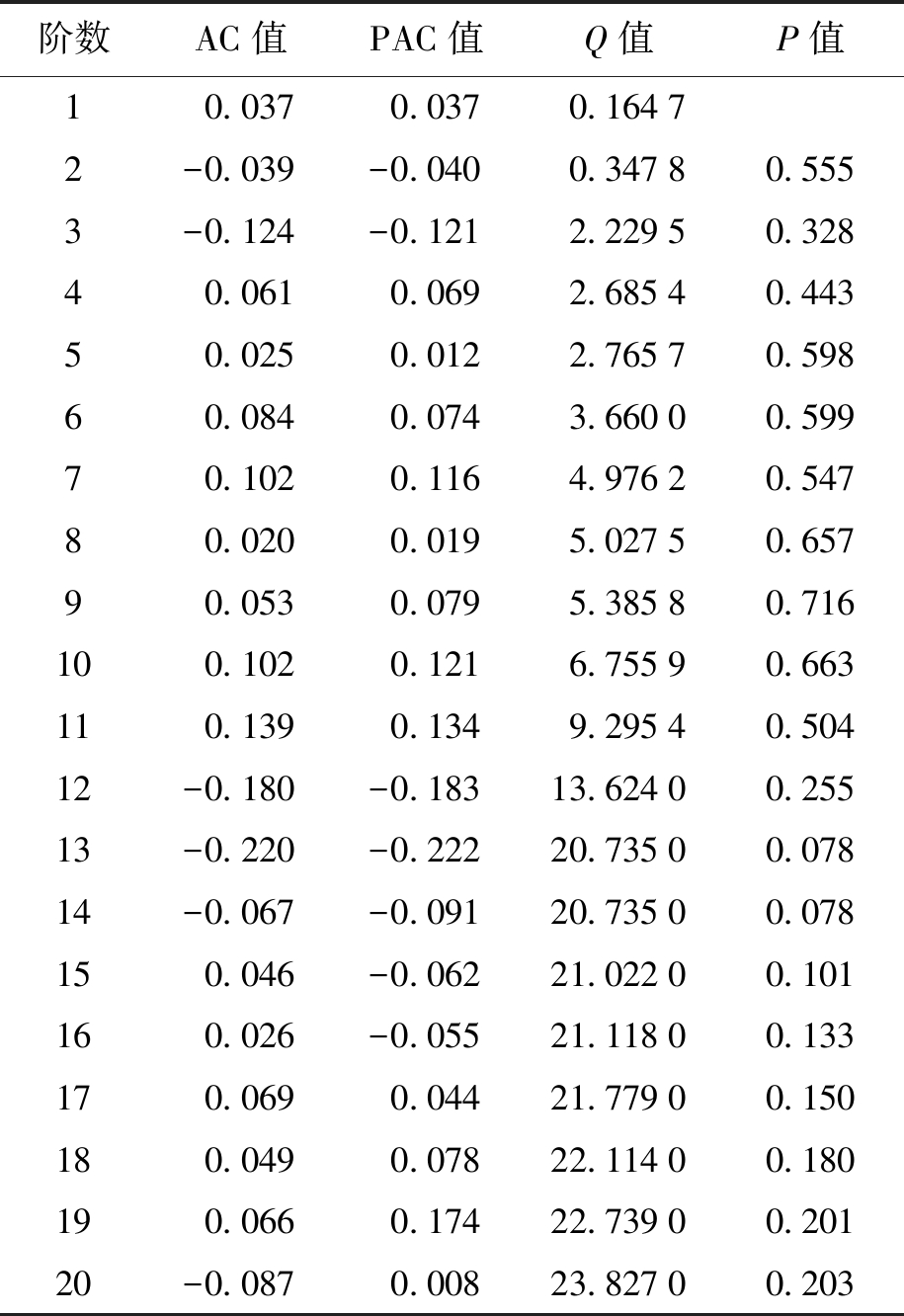
阶数AC值PAC值Q值P值10.0370.0370.16472-0.039-0.0400.34780.5553-0.124-0.1212.22950.32840.0610.0692.68540.44350.0250.0122.76570.59860.0840.0743.66000.59970.1020.1164.97620.54780.0200.0195.02750.65790.0530.0795.38580.716100.1020.1216.75590.663110.1390.1349.29540.50412-0.180-0.18313.62400.25513-0.220-0.22220.73500.07814-0.067-0.09120.73500.078150.046-0.06221.02200.101160.026-0.05521.11800.133170.0690.04421.77900.150180.0490.07822.11400.180190.0660.17422.73900.20120-0.0870.00823.82700.203
3. 价格预测
利用模型对2017年1月—2018年3月的玉米价格进行短期预测,并与真实数据进行对比,结果如表6所示。由表6可知,玉米的真实价格与预测价格的误差很小,绝对误差最大为0.06,平均误差率为1.359%,说明预测值和真实值比较接近,可以用此模型进行短期的预测。另外,利用此模型作向前一期的预测,可得4月份玉米价格为2.06元/千克。与2017年相比,2018年一季度的玉米价格不仅突破了2元/千克,并且短期内会有小幅度的上升。
四、结论与建议
(1) 将2007年1月—2018年3月我国玉米平均月度价格序列作为研究对象,利用X12季节调整法和H-P滤波法将其分解为长期趋势序列、季节因素序列、随机因素序列和循环趋势序列,研究其波动规律。结果发现,在研究区间内玉米价格受季节因素影响较大,整体价格趋势为先上升后下降,并且呈现周期性波动,平均每三年为一个波动周期,波动幅度趋于稳定。
表6 预测值误差
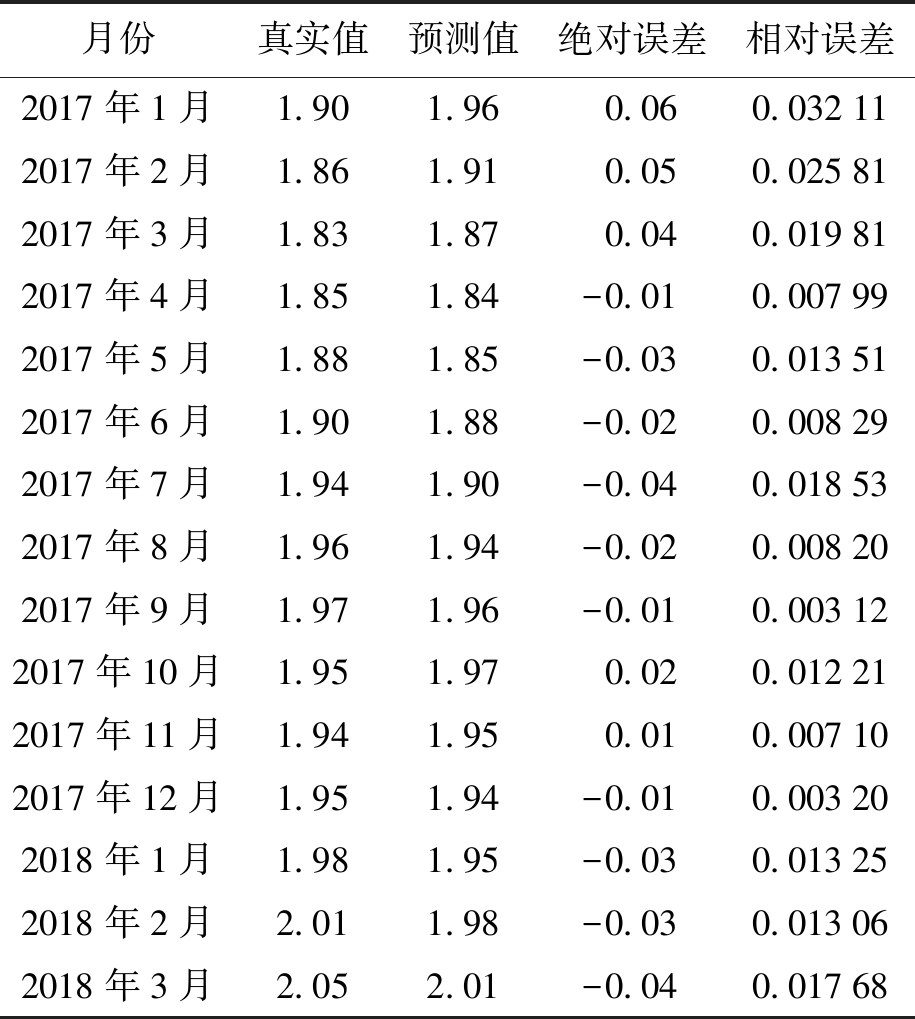
月份真实值预测值绝对误差相对误差2017年1月1.901.960.060.032112017年2月1.861.910.050.025812017年3月1.831.870.040.019812017年4月1.851.84-0.010.007992017年5月1.881.85-0.030.013512017年6月1.901.88-0.020.008292017年7月1.941.90-0.040.018532017年8月1.961.94-0.020.008202017年9月1.971.96-0.010.003122017年10月1.951.970.020.012212017年11月1.941.950.010.007102017年12月1.951.94-0.010.003202018年1月1.981.95-0.030.013252018年2月2.011.98-0.030.013062018年3月2.052.01-0.040.01768
(2) 建立ARIMA模型对玉米未来价格进行短期的预测,与真实价格对比误差较小,说明模型具有参考意义,且预测玉米价格在短期内会有小幅度的上升。另外,对玉米价格的预测还应综合考虑政策、天气等因素的影响。
(3) 自取消玉米临储政策以来,玉米价格持续走低,预测2018年开始小幅度回升,说明新的玉米定价机制已步入正轨,玉米价格稳中有进。深化玉米供给侧改革有利于玉米行业稳定健康发展,应鼓励农民种植种类多样化,加快玉米深加工,以减少玉米库存。
[1] Moore H L.Forecasting the yeild and the price of cotton [M].New York:The Macmillan Company,1917.
[2] Sarle C F.The forecasting of the price of hogs [J].American Economic Review,1925,15(3):1-22.
[3] Chen Y C,Rogoff K S,Rossi B.Predicting agricommodity prices:an asset pricing apporach [J].Scorn Electronic Jounrnal,2010(2):45-54.
[4] Talawar V M.Market dynamic and price forecasting of maize in South Karnataka:an application of Garch model [D].Dharwad:University of Agricultural Sciences,2010.
[5] Jha G K,Sinha K.Agricultural price forecasting using neural network model:an innovative information delivery system [J].Agricultural Economics Reseach,2013(26):229-239.
[6] 余洁,韩啸,刘芳,等.我国生鲜乳价格波动周期分析 [J].中国奶牛,2014(18):30-33.
[7] 李哲敏,李干琼.2012年我国禽蛋市场分析与展望 [J].中国食物与营养,2013,19(5):40-42.
[8] 李敏,胡继连.基于Census X12和ARIMA模型的香菇价格波动特征分析——以山东省为例 [J].中国食用菌,2016,35(2):71-76.
[9] 王素雅.农产品短期价格分析及预测方法选择——以北京新发地批发市场苹果为例 [D].北京:中国农业科学院,2009.
[10] 李正辉,陆芸,何融.农产品价格周期性波动研究——基于小波分析 [J].调研世界,2013(5):39-41.
[11] 陈灿煌.我国农产品价格指数短期预测——基于时间序列分解的分析 [J].价格理论与实践,2011(7):55-56.
[12] 张婷.CPI的SARIMA模型与X-12季节调整模型对比预测分析 [J].经济问题,2014(12):37-41.
[13] 范青青,袁艳红.基于X12-ARIMA模型的猪肉价格波动规律研究 [J].畜牧经济,2018,54(6):137-142.
[14] 杨斌清,张贤平.稀土氧化物价格波动周期分析——基于X12季节调整和H-P滤波模型 [J].中国稀土学报,2016,34(3):354-362.
[15] 王雨琴.季节调整方法比较研究——基于中国月度CPI序列 [D].广州:暨南大学,2016.
[16] 韩振,杨春.供给侧背景下我国玉米价格走势预测 [J].价格理论与实践,2017(11):99-102.
[17] 滕永平,周婷婷.大豆期货价格预测实证研究 [J].沈阳工业大学学报(社会科学版),2017,10(4):331-334.
[18] 刘红亮.重庆市短期保费收入预测模型探析——基于季节调整法和ARIMA模型 [J].财经纵横,2013(16):130-131.
[19] 颜伟,程超,薛斌,等.结合X12乘法模型和ARIMA模型的月度电量预测方法 [J].电力系统及其自动化学报,2016,28(5):74-80.
[20] 罗丹程,黄月,王添钰.我国白糖期货价格和现货价格关系的实证研究 [J].沈阳工业大学学报(社会科学版),2016,9(5):399-413.
[21] 易丹辉.数据分析与Eviews应用 [M].2版.北京:中国人民大学出版社,2014.