近年来,数据驱动等技术的快速发展催生了许多诸如互联网保险定价等创新业务模式。区别于传统的互联网保险产品定价,中小保险公司由于自身规模及技术的限制,在用户冗杂的数据群中如何简明有效地获取定价数据变得尤为困难,使得传统的保险精算定价已经不能满足市场的庞大需求。此外,由于互联网保险起步时间较晚、历史数据不足,对于某项具体互联网保险进行保险产品设计也存在着较大的风险。
一、文献回顾
在保险领域的研究中,最早由Merton(1977)将期权定价方法应用于存款保险的研究。Coppola通过建立一个滚动窗口仿射随机模型,引入了时间死亡率波动率的时间结构作为寿命冲击的驱动因素,来研究长寿风险的偿付能力Ⅱ所表示的偿付能力资本要求[1]。该研究包含了长寿冲击相对于监管模型假设的年龄和时间的不变性所导致的扭曲和不一致问题,推导出寿命冲击作为死亡率时间波动演化和时间的函数,提出一种衡量保险业偿付能力资本要求的期权定价方法。
彭红枫等利用期权定价方法对防癌险进行了研究,提出了相应的定价思路[2]。王继霞等研究出随机利率下B-S模型基于非参数估计的期权保险精算定价模型[3]。祝丽萍等基于幂期权的行权特点,构建了分形布朗运动驱动下的保险期权定价模型[4]。王小莹等构建了随机利率模型下的几何平均亚式期权定价方法[5]。武涛等利用保险精算方法,推导出双分数Ornstein-Uhlenbeck过程下欧式幂型期权和欧式上封顶及下保底幂型期权定价公式[6]。李浩然等研究出随机利率跳扩散模型期权保险定价解析表达式[7]。周孝华等给出了修正的Black-Scholes存款保险定价公式[8]。梁喜珠等研究得出了次分数跳扩散过程下最值期权的定价公式[9]。李子耀等实现了B-S和二叉树两种期权定价模型在财产险定价中的应用[10]。陈聪等结合改进的蒙特卡洛法和矩近似解析法,得到了算术平均半亚式期权定价的近似半解析法,在确保精度的前提下大幅减少了计算时间[11]。
在财产保险方面引入期权定价的研究较少,大多是对保险精算定价的理论研究,很少有研究与具体财产保险相结合。张晓倩等改进了以往研究成果中保险精算价格的定义公式,在假定标的资产价格服从指数Ornstein-Uhlenbeck(O-U)过程、利率服从Vasicek利率模型的基础上,利用随机分析知识获得了再装期权的保险精算价格公式[12]。石方圆等则更进一步设计出随机利率及O-U条件下关于保险精算的彩虹期权定价公式[13]。彭梅等结合不确定理论,对参数依赖时间的欧式期权按照保险精算方法定价,最后得到了接近市场且符合无套利原理的期权价格[14]。张耀杰等对障碍期权下的贷款保险进行了研究,表明违约门槛上升与保险定价水平呈现某种正相关关系[15]。赵月旭等采用鞅方法等,得到了对数正态带跳扩散模型下美国巨灾灾害欧式看涨保险期货期权在任意时刻的定价公式,验证了保险精算定价是一种较为合理的定价方法[16]。
上述文献从不同角度对保险定价问题进行了研究,但现有研究中较少有建立具体保险产品价格模型、将保险定价方法与实际险种相结合的内容。本文以机动车交通事故责任强制保险(交强险)为例,立足于无套利原理、蒙特卡洛模拟等产品定价方法,结合互联网财产险保险合约设定定价模型,通过模拟机动车交强险发生事故序列随时间变化路径,考虑机动车交强险特殊敲出条件及投保人每期花费保费数额与上一年度车险事故发生序列有直接关系。根据保险公司年平均最终出险率进行蒙特卡洛模拟,构造出保险事故Pt序列,再通过具体的Pt序列求出对应保单的费用,最终计算出平均费用即为理论定价价格X。
对于其他与本文定价模型较为相近的保险条款,只需进行适当的变量及模型形式变化,也同样适用定价。本文模型具有很好的适用性及定价效率,能够为具体财产险险种进行有效定价。
二、问题描述
从保险产品的本质出发进行探讨,保险公司所得到保费现金流受保险状态影响较大,期权组合的方式有利于降低现金流的影响。传统保险产品影响因素较多,而对其使用期权组合的方式时所需的条件又相对复杂,所以大多数学者在前期对于存款保险的研究较多,并未将期权定价方法在后期具体的保险险种研究中进行具体应用。随着互联网行业的发展,互联网保险的行业优势逐渐显现[17-18]。传统保险精算定价方法为了给每一细分的保险产品制定定价策略,需要进行大量重复的精算,对于保险公司而言,其工作量及保险产品开发成本无疑是巨大的[19]。所以,基于互联网保险自身的特点,开发快速准确的保险定价方法显得非常重要。
考虑到互联网保险中占比较大的为消费型互联网保险产品,同时具备较为明晰且类似的期权结构,本文以机动车交强险为主要研究对象确定基本定价模型,并扩充更为丰富的保险条款以扩展基本的定价模型,从而进一步扩宽互联网财产险产品范围,更为准确地确定定价标准。
考虑到互联网财产险的实际保险情况及具体期权的特点,研究所采用的期权结构为欧式看涨障碍期权,即投保人每期花费一定数额保费去购买一个看涨障碍期权,这里的行权日即保险事故发生日。对于机动车交强险这种需要在每期一交费、其后续续费与否取决于上期的保险产品来说,可以把它看作若干持续期组成的期权结构化产品。这种期权结构本身附带有结束合约的敲出条款。例如,机动车交强险的一个普遍敲出条款就是:投保人所投保的车辆每年发生交通事故的次数超过4次,则此后整个保险合约终止,保险公司不再承保该保险标的。
正是基于对互联网财产险所蕴含的期权结构和相应的保险条约的分析,本文以机动车交强险为研究基础,充分发挥该险种覆盖面广的优势,力争确定更为全面准确且后期可扩展的定价模型。以此为指导对不同互联网财产险产品进行定价,助力解决传统中小保险企业在自身规模及技术尚不全面的情况下对于互联网财产险的定价需求。
三、模型构建
以机动车交强险为例,探究互联网财产险产品定价。为了定义机动车交强险的期权结构,需要从具体保险合约中进行深入探索,归纳总结出其所具有的期权结构。
1. 交费期、保障期及等待期
通常保险公司在机动车交强险方面执行相同的费率标准,且将机动车交强险交费期设置为每期一交费(一期通常为一年),每期交费后即享有相应的一年保障期。如果需要更长时间的保障,投保人在未触及保险合约敲出条款的情况下可连续每期购买。本文假设机动车最长使用年限T为15年。可持续交费期的期间长度与上一年度被保险车辆发生保险事故次数有关,一般来说,上一年车辆出险次数不超过4次,保险公司一般会同意一直续保。但若出险次数过多,保险公司会考虑提高费率标准或不续签合约。
保障期是指投保人购买机动车交强险之后,如果在保障期内发生保险事故,投保人及时报险,保险公司在等待期内进行确认无误后,可以获得保险公司赔付,此为一次保险赔付的完成。但投保人在该保障期内投保的保险合同并未就此终止。
机动车交强险价格按照车辆的大小进行确定,每期所交保费数额与上期出险次数有着一定的正相关关系,上期出险次数越少则本年保费获得的优惠越多。其中规律就是上一年度出险次数越多,则下一年度所交保费总额越高。假定所研究的机动车交强险不涉及脱保、过户等使得保费中断重新计算的情况,保费与机动车大小、出险次数具体关系如表1、2所示。
表1 交强险中机动车座位数与交费时间关系 元

年份5座6~8座第1年9501100第2年855990第3年760880第4年665770第5年665770
资料来源:平安保险有限公司官网。
表2 机动车出险次数与保费折扣关系 %
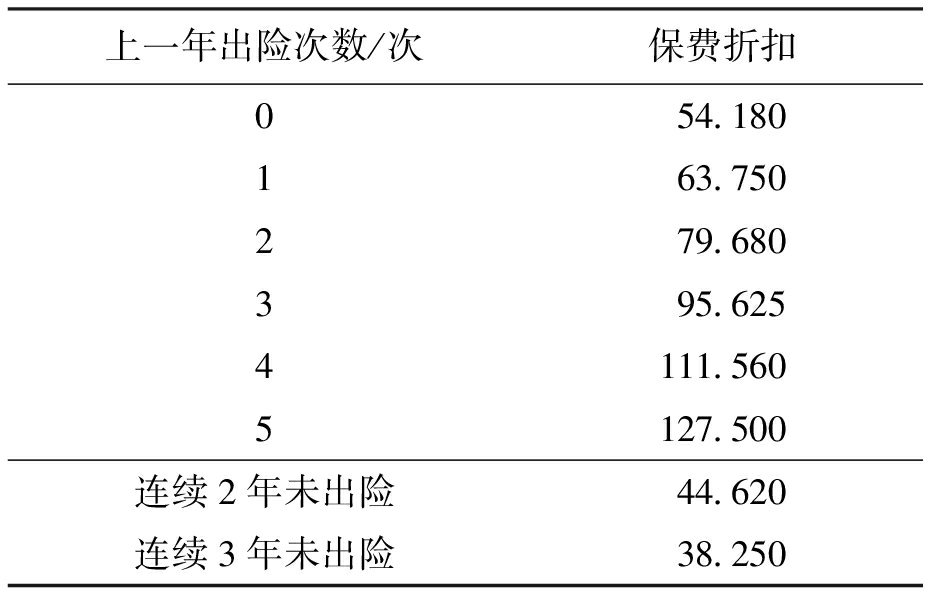
上一年出险次数/次保费折扣054.180163.750279.680395.6254111.5605127.500连续2年未出险44.620连续3年未出险38.250
资料来源:平安保险有限公司官网。
等待期是指保险人收到被保险人的索赔请求后作出核定所需要的时间。通常对于机动车交强险而言,保险事故发生后,被保险人应根据事故性质和损失情况及时向保险人提供索赔须知。等待期相对于保险期间而言时间较短,且一般都能及时赔付,所以本文对等待期这一期间忽略不计。
2. 互联网财产险种类与赔付
目前在售的互联网财产险种类丰富多样,各财产险险种保险条款亦十分详细,保额保费各不相同。按照互联网财产险所占市场份额划分,可以将互联网财产险分为互联网车险与互联网非车险两部分。
保费收取大致规律:保险公司会对财产毁损发生率和保额作出权衡比较,保费由保险金额、保险费率和保险期限构成。保险金额与保险费率和保险期限成正相关关系,即保险金额越大,费率越高,保险期限也越长。从现有的机动车交强险产品来看,机动车交强险赔偿最高责任限额为11万元,而无责任情况下最低限额为100元。也有部分机动车险采取较为一致的赔付标准,具体和机动车保险期限等因素差异不大。2009—2017年间,占车险业务量最大的机动车交强险最终平均出险率为13.10%。按照保险公司对不同年份机动车交强险保额的设定,其规律就是对于不同年份机动车交强险出险率赔付的总额较为一致。也就是说,不同保险公司机动车交强险出险率虽略有差异,但按照每个保险公司的数据进行计算,保额赔付会得到一致的结果。
考虑机动车保险中业务量规模大小,业务量前三名分别是机动车交强险、车损险、第三者责任险。又考虑到机动车交强险在实际过程中每年保险公司最终出险率统计偏差不大,因此分析中使用机动车交强险的数据要明显优于机动车其他险种数据,既保证了数据统计的一致性,又使得统计研究对所有保险公司有较为一致的针对性与适用性。基于无套利原理思想可以得知,不同保险公司最终机动车交强险出险率与对应保额的乘积得到的现金流是一致的,所以利用不同保险公司交强险出险率数据进行定价研究时,其结果是无差异的。
于是,设定的期权定价模型中有这样的假设:每期保险公司对机动车交强险赔付总额的期望值一致。对中国人民财产保险有限公司、中国人寿财产保险有限公司、中国平安财产保险等十家保险公司机动车交强险最终出险率数据进行统计(见表3)。限于数据的连续性与完整性,统计数据选取年份为2009—2017年。
表3 机动车交通事故责任强制险最终出险率统计 %

保单年度中国人民财产保险中国人寿财产保险中国太平洋财产保险中国平安财产保险中国大地财产保险华泰财产保险阳光财产保险中华联合财产保险永安财产保险华安财产保险200913.8015.3015.9016.209.5015.909.4414.4012.9010.60201012.2013.1014.7016.8010.0014.309.1411.9012.0011.80201112.8012.6014.2016.6010.0014.6010.1111.7010.9010.60201215.2013.2015.2016.5010.5014.5011.6112.7011.0010.60201315.4013.0016.2016.1010.2014.0011.6912.5010.109.90
表3(续) %
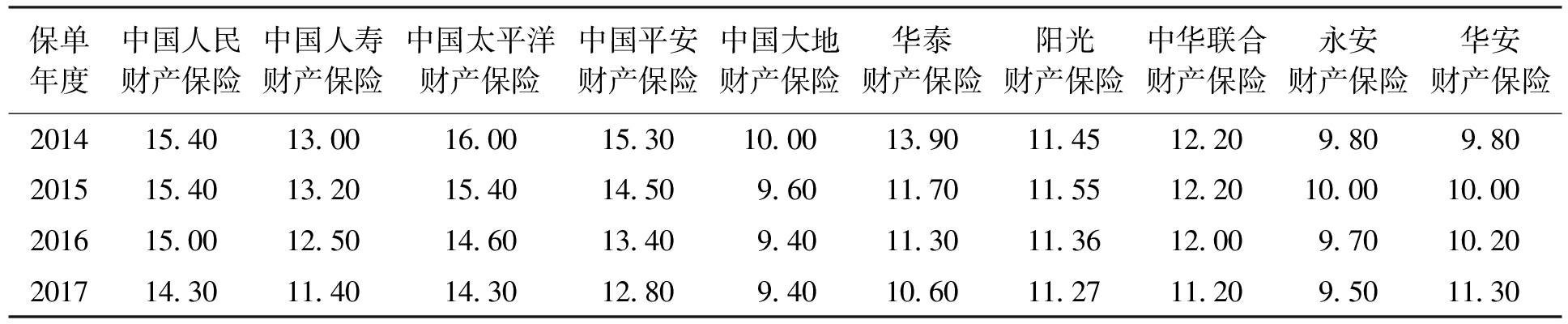
保单年度中国人民财产保险中国人寿财产保险中国太平洋财产保险中国平安财产保险中国大地财产保险华泰财产保险阳光财产保险中华联合财产保险永安财产保险华安财产保险201415.4013.0016.0015.3010.0013.9011.4512.209.809.80201515.4013.2015.4014.509.6011.7011.5512.2010.0010.00201615.0012.5014.6013.409.4011.3011.3612.009.7010.20201714.3011.4014.3012.809.4010.6011.2711.209.5011.30
资料来源:根据中国保险业协会网站数据整理。
3. 敲出条款
敲出条款,即保单终止的条款。机动车交强险保险条款中均会规定:投保人在投保后,在符合保险条约出险后赔付情况下,当投保人所投保车辆出险不超过一定次数时,保险公司在下一年会同意续保;但如果上一年出险次数过多,保险公司则会终止下一年的保险合约续约。保险合同何时终止,取决于投保标的上一年的保险情况,而不是本年所发生的保险次数。保险人在支付约定保额的赔付后,不退还投保人之前所交的保费。
4. 意外情况
对于发生如地震及其次生灾害、战争暴乱等不可抗力的意外情况,一般属于保险公司的免责条款,无论损失程度如何,保险公司均不予赔付。但此类意外不影响保险持续期内其他出险情况的赔付,保险标的物灭失的除外。由于此类意外情况在实际生活中发生概率较小,故本文不考虑其产生的影响,不作具体探讨。
5. 互联网财产险的期权结构
设某个机动车交强险保障期为t。将每个保障期t看作1年,投保人持续续约期为T。考虑到机动车交强险单期交费的特点,设定单期费用为X,在此保障期内发生约定出险情况则获得保险赔付。保险合约期满,根据上一年情况,符合保险公司保险条约要求的可以续约,费用为αtX(αt为保险公司按去年情况决定的上下浮动比例)。这种保险合同可以看作一种结构性期权产品,由一个具有特殊条件的T期看涨期权构成,该期权产品的期限也为T。
也就是说,若投保人一共续约T期,其实相当于投保人每期花费αtX购买一个看涨障碍期权。对于投保人而言,该时期内看涨障碍期权的现金流为
(1)
式中:Pt为车险事故发生序列,如Pt=0,说明第一年并未发生车险事故;M为合同规定的赔付金额。
投保人在约定期间内发生约定保险事由后,获得的赔付额为PtM。同时,该期权附带的特殊敲出条款是:当约定保险事故发生时,期权行权,投保人获得相应保额赔付,投保人下一年度所交保费数额与上一年车险事故发生序列有关。但在此种情况下隐含的一个事实,就是该保险标的未曾在保险期间内灭失,否则之后保险期间持续期内车险事故发生序列停止计算,该保险合约的可持续期也自动终止。这类特殊敲出条款影响着交强险的期权结构路径,看涨障碍期权的实际价值影响因素变得复杂,也不利于投保人准确分析期权产品的价值,容易发生盲目投保现象。
因此,选取保险公司而非投保人为主体进行研究分析。分析中涉及上文保险续费费用αtX中的参数αt序列与Pt序列相关,具体表现为

(2)
若连续多年未发生事故则有进一步优惠
(3)
假设无风险利率r为4%,投保总人数为100 000,事故发生率为Nt。对于保险公司来说,每卖出一份保单就会得到一笔保费收入。将保险公司和投保人之间的保险合同视作包含特殊敲出条件的一系列期限为T的结构化期权产品。保险公司在整个持续期T内获得的保费收入额为
(4)
同时,在持续期内保险公司该保险合约现金流出贴现值为
(5)
式中,X为所需缴纳的单期保险费用;Nt为该保险合约当年发生赔付的人数;Q为赔付次数的频率分布。
由于保险公司对于用户数据的保密性原则,本文并未获得Q的真实数据,此处出险次数频率Q为假定值。同时需要说明的是,Q也是一个变化的值,实务中保险公司借助数据驱动技术,依托历史数据的变化可以较为精准地预测到每期Q分布频率,具体如表4、5所示。
表4 出险次数与频率关系
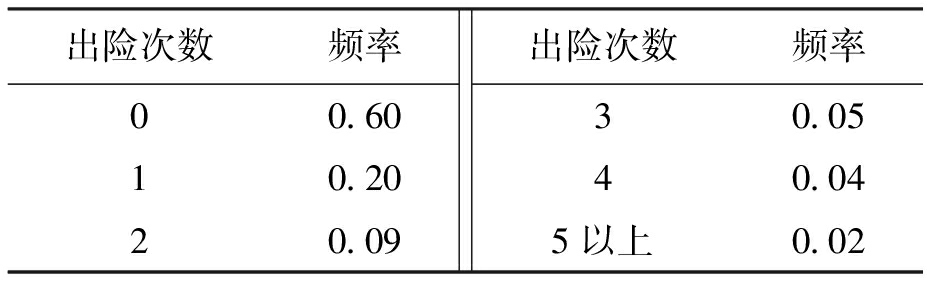
出险次数频率00.6010.2020.09出险次数频率30.0540.045以上0.02
表5 0次出险频率假定构成

未出险时长频率1年0.6连续2年0.3连续3年0.1
根据无套利原理,有
PVCI=PVCO
(6)
即
(7)
对式(7)求解,可得在该Nt序列下的保单费用X。
该方程的求解重点在于Nt序列。根据保险公司统计的历年最终出险率数据进行蒙特卡洛模拟,从而构造Nt序列;再通过具体的Nt序列,求出相应的保单费用;最终计算平均费用即理论价格,表示为
(8)
四、仿真与分析
1. 蒙特卡洛数值模拟框架
选取2006—2017年各保险公司机动车交强险最终出险率来完成Nt序列的构建,数据如表6所示。
表6 2006—2017年机动车交强险最终出险率 %

年度中国人民财产保险中国人寿财产保险中国太平洋财产保险中国平安财产保险中国大地财产保险华泰财产保险阳光财产保险中华联合财产保险永安财产保险华安财产保险年均值200610.80--12.70-17.30----13.60200713.9022.9016.0015.70-20.10-17.70-10.2016.64200814.4018.5016.1015.90-14.00-16.00-9.1014.86200913.8015.3015.9016.209.5015.909.4414.4012.9010.6013.39201012.2013.1014.7016.8010.0014.309.1411.9012.0011.8012.59201112.8012.6014.2016.6010.0014.6010.1111.7010.9010.6012.41201215.2013.2015.2016.5010.5014.5011.6112.7011.0010.6013.10201315.4013.0016.2016.1010.2014.0011.6912.5010.109.9012.91201415.4013.0016.0015.3010.0013.9011.4512.209.809.8012.69201515.4013.2015.4014.509.6011.7011.5512.2010.0010.0012.36201615.0012.5014.6013.409.4011.3011.3612.009.7010.2011.95201714.3011.4014.3012.809.4010.6011.2711.209.5011.3011.61
注:-表示官网未收录或统计该数据。
根据以上各保险公司年平均最终出险率的历史数据,可以对Nt序列进行模拟。假定最终出险率N服从布朗运动
dN=μdt+σNdz
(9)
式中:μ为N历史序列变动率的期望;σ为N的波动率,是历年最终出险率变动比例的标准差,代表最终出险率的波动;dz为维纳过程。
将式(9)的连续模型进行离散化可得
(10)
则![]() 很接近,且N(t0),N(t1),…,N(tn)为相互独立的正态随机变量。考虑到实际应用中模拟的精确性,模拟并不是从N(t)入手,而是从N(t)的对数ln N(t)入手,因为可以很快得到
很接近,且N(t0),N(t1),…,N(tn)为相互独立的正态随机变量。考虑到实际应用中模拟的精确性,模拟并不是从N(t)入手,而是从N(t)的对数ln N(t)入手,因为可以很快得到![]() 也呈正态分布,即ln N(t1)-ln N(t0),ln N(t2)-ln N(t1),…,ln N(tn)-ln N(tn-1)也是呈正态分布的相对独立的随机变量。
也呈正态分布,即ln N(t1)-ln N(t0),ln N(t2)-ln N(t1),…,ln N(tn)-ln N(tn-1)也是呈正态分布的相对独立的随机变量。
根据伊藤引理,有
(11)
将上述随机过程改写为离散形式有
(12)
进而可以推知
(13)
式中,ε为一个标准正态分布随机变量。
根据式(11)~(13)进行Nt序列的模拟。每一次模拟都能给出未来某个持续期内该保险合约当年发生赔付人数,进而代入公式求出保单的费用,最终计算出的平均费用即为该保险产品理论价格。
定价方程(1)~(3)、(7)、(8)、(13)构成本文的基准定价模型。对方程(13)进行大量蒙特卡洛模拟得出Nt序列,然后代入式(7)求得保险产品定价的解。
2. 仿真结果分析
在具体仿真实验中,选取不同的持续期T(5,10,15,单位为年)和不同机动车交强险约定获赔保额M(5 000,10 000,单位为元),并针对不同T、M的组合分别设定模拟次数。每次进行5 000次蒙特卡洛模拟来计算保费价格X,每次模拟都可以计算出保险合同在一个连续时期内的索赔数量。将模拟的Nt序列代入式(7)得到机动车交强险保费近似值X。机动车交强险保险实务中发生保险事故后获得的保额受各种具体情况限制,所以保险公司才约定某种出险具体情况所对应的获赔保额是不同的。以5 000元、10 000元两种获赔保额为例进行运算,其他情况同理。
图1a~f是在保险金额分别为5 000元、10 000元的情况下,对不同持续时间的模拟定价结果。
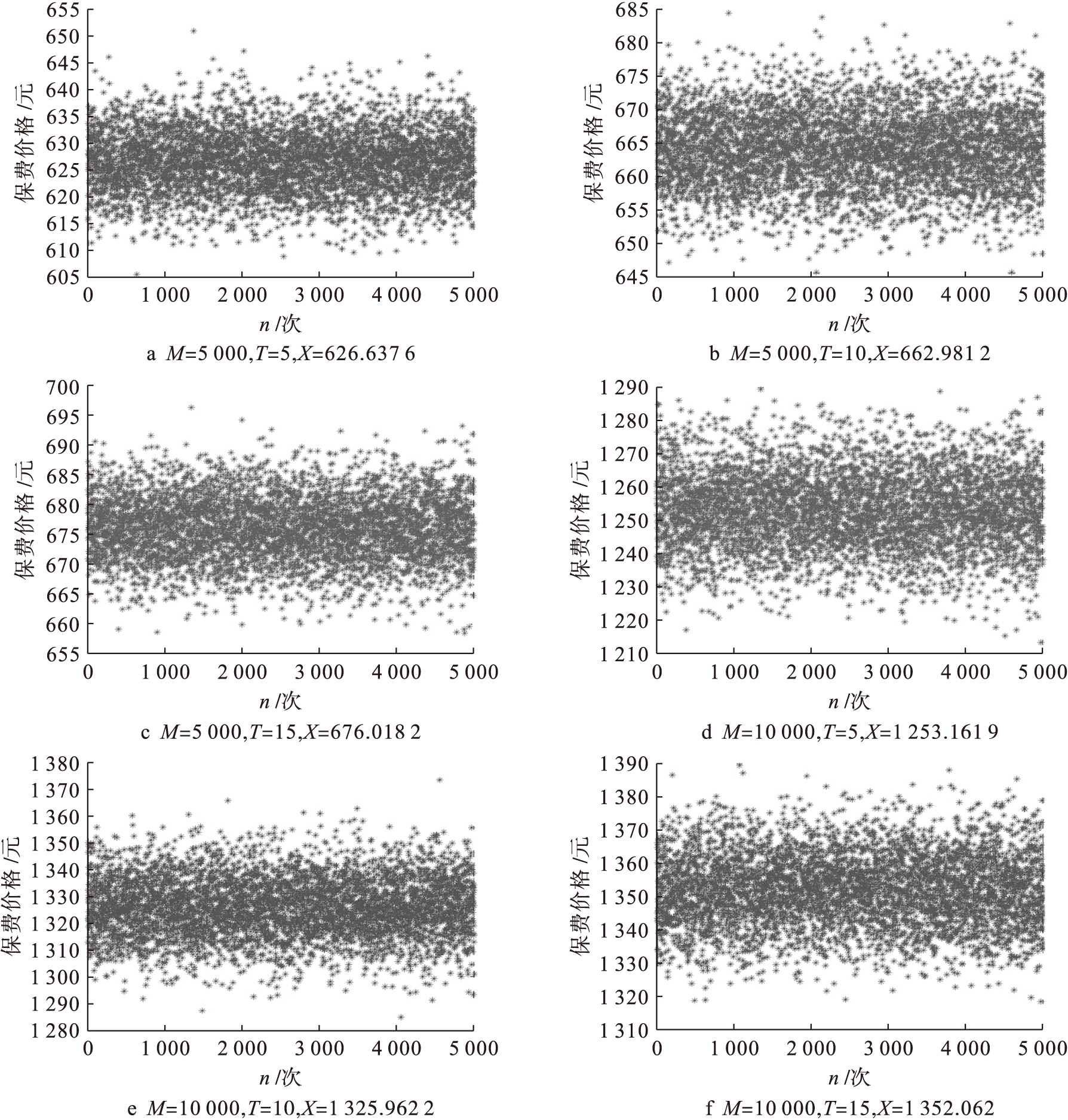
图1 机动车交强险数值模拟定价结果
从定价结果来看,本模型定价结果与保险公司实际业务中的定价结果相近,有略微差值的为设定的保险事故某期发生次数的对应赔付概率。在保险条约具体给定的情况下,可以根据获赔保额或应交保费任意值推算另一值,甚至可以做到三者之间的相互可逆推算。
在定价的时间效率方面,本文提出的数值模拟方法可以快速对机动车交强险进行保险定价,避免了传统保险定价策略的大量重复计算,且实务中可运用大数据技术实时更新保险事故某期发生的赔付次数,使得定价更加准确,为中小保险企业提供新的定价思路与策略。
3. 静态比较分析
由于无法给出所有互联网财产险产品定价模拟的结果,上文只选用和财产保险较为相似的机动车交强险同模拟价格进行比较。为了更好地探讨出保险期限、获赔保额及保费之间的关系,进一步进行静态比较分析。考虑到机动车交强险最大持续期及实际获赔保额情况,选取T为3~15年,获赔保额M为5 000元~12 000元这一范围数据,对不同T-M组合进行数值模拟。持续期T、获赔保额M与保险产品定价之间的关系如图2所示,其更为形象地显示了三者的关联关系。
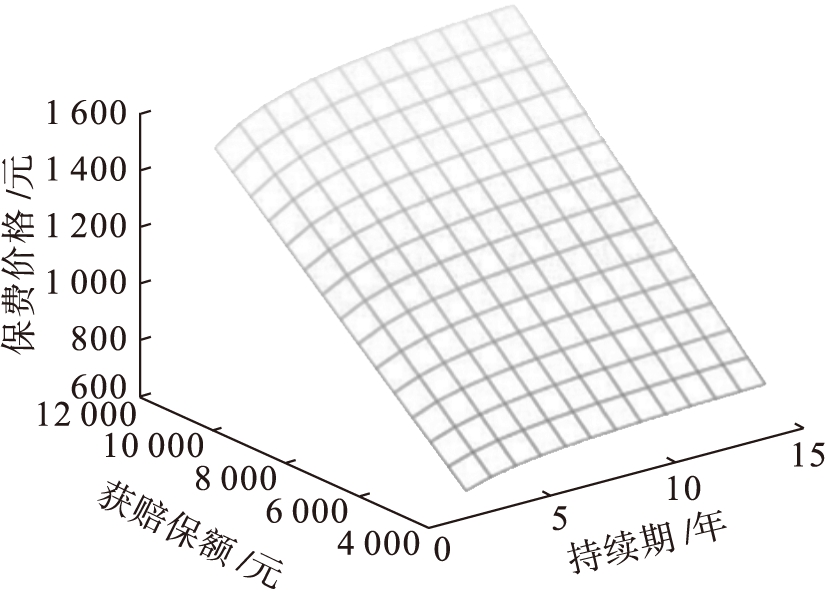
图2 不同保额及持续期组合下机动车交强险数值模拟定价结果
五、针对互联网财产险的定价模型扩展
为使定价模型更加适用于高度细分的互联网财产险定价,有必要对定价模型进行扩展,为中小保险公司互联网财产险的定价策略提供更多的参考。以机动车交强险为例的期权定价模型为基础,对保险合约有所差异的其他互联网财产险产品定价应用作探讨补充。
1. 对定价模型的应用性扩展
由于不同的互联网财产险险种所对应的具体保险合约细节有所差异,反映在定价模型中就需要对一些参数和定价模型的形式进行微调。合约细节或形式越贴近,则保险定价模型的适用性越强。实际应用中需将不同险种保险合约与机动车交强险进行比较,根据其不同之处对定价模型进行微调处理,以适应更多险种。
若某类互联网财产险与机动车交强险合约细节类似,则不需对模型作较大改动,只需对这些财产险的交费期、保障期、费率等数值进行替换,并将Nt序列替换为所求险种对应的标的序列,之后便可根据上文方法对此类互联网财产险进行定价。
若某类互联网财产险为返还型互联网保险,比如到期还本型的房屋财产险,虽保险合约与机动车交强险有所差异,条款也更加复杂,但期权结构相似且并无本质区别,则只需将到期还本的本金按分期累计的方式加到赔付项中即可。
2. 保险期权定价中利率模型的作用探讨
期权定价理论中,一些学者讨论了利率模型的作用。在本文实证研究过程中,针对不同利率模型参考了大量文献并进行分析,但最终结果显示其并无较好的适用性。综合来看,若讨论的是历史利率对于定价模型的影响,则历史年份利率均可获得,没有引入利率模型的必要性,根据历史利率数据验证模型的合理性即可。若考虑引入一个利率模型推算未来利率,由于机动车交强险交费期较短(一般为一年)、利率波动幅度较小,只推算出未来一年利率意义不大。因此利率模型在保险期权定价中作用不大,本文也并没有引入利率模型加以计算,更多地是依据现有利率验证过去定价适用性,为互联网财产险险种保单定价提供参考。
六、结 论
本文以机动车交强险为例,研究了互联网财产险险种包含的期权结构,并采用蒙特卡洛模拟及无套利定价方法对互联网财产险产品进行定价,提出了路径依赖型具有复杂期权结构的互联网财产保险产品的定价模型。通过定价结果分析,得到了符合实际预期的险种价格定价区间,验证了该模型的定价能力。对于具有类似保险合约的互联网财产险,只需对定价模型中的参数及方程形式进行微调便能广泛应用。考虑到不同互联网财产险保险合约的差异性,对具有不同保险合约的互联网财产险定价进行了思路扩展。
本文基于蒙特卡洛数值模拟所提出的定价模型具有较好的适用性与扩展性,并利用数据驱动对赔付概率进行及时调整,满足了时效性需求,为创新转型阶段的传统中小保险企业提供了一种新的定价思路,以满足不同细分的保险市场需求。
[1]Coppola M D,Amato V,Levantesi S.An option pricing approach for measuring solvency capital requirements in insurance industry [J].Physica A:Statistical Mechanics and its Applications,2018(2):509-521.
[2]彭红枫,肖祖沔.互联网保险的期权定价框架——基于Monte Carlo数值模拟分析 [J].保险研究,2016(5):36-47.
[3]王继霞,王添秀.随机利率下B-S模型基于非参数估计的期权保险精算定价 [J].郑州大学学报(理学版),2018,50(3):94-99.
[4]祝丽萍,崔朝剑雄,张胜,等.分形布朗运动驱动下幂期权的保险精算法 [J].昌吉学院学报,2018(6):100-103.
[5]王小莹,王玉文.随机利率模型下几何平均亚式期权的保险精算定价 [J].哈尔滨师范大学自然科学学报,2018,34(1):1-3.
[6]武涛,薛红.双分数Ornstein-Uhlenbeck过程下欧式幂型期权定价模型 [J].西安工程大学学报,2018,32(3):370-376.
[7]李浩然,姚素霞.跳扩散模型随机利率下期权的保险精算定价 [J].安阳师范学院学报,2018(4):24-26.
[8]周孝华,熊云飞.基于修正Black-Scholes期权定价模型的存款保险定价探微 [J].财会月刊,2017(12):53-57.
[9]梁喜珠,薛红,王瑞.次分数跳![]() 扩散环境下最值期权定价 [J].四川理工学院学报(自然科学版),2019,32(5):80-86.
扩散环境下最值期权定价 [J].四川理工学院学报(自然科学版),2019,32(5):80-86.
[10] 李子耀,黄洪瑾.B-S和二叉树两种期权定价模型在财险定价中的应用与比较 [J].上海立信会计金融学院学报,2017(5):104-111.
[11] 陈聪,唐亚勇.算术平均半亚式期权的快速定价算法 [J].四川大学学报(自然科学版),2020,57(6):1061-1066.
[12] 张晓倩,刘会利.随机利率下基于O-U过程的再装期权保险精算定价 [J].河北师范大学学报(自然科学版),2020,44(6):479-485.
[13] 石方圆,杨立保,李翠香.基于带跳的O-U过程的彩虹期权定价 [J].合肥工业大学学报(自然科学版),2017,40(12):1714-1718.
[14] 彭梅,李翠香.不确定理论下期权的保险精算定价 [J].经济数学,2017,34(3):84-87.
[15] 张耀杰,史本山.基于障碍期权的贷款保险定价研究 [J].运筹与管理,2018,27(6):148-155.
[16] 赵月旭,刘洁.美国巨灾灾害保险期货期权的鞅方法定价 [J].数学的实践与认识,2019,49(22):16-21.
[17] 于娇,丛闻,李雄勇,等.“互联网+”驱动辽宁装备制造业产业升级研究 [J].沈阳工业大学学报(社会科学版),2020,13(4):312-317.
[18] 袁峰,刘玲,邵祥理.第三方网络平台人身险投保意愿影响因素研究 [J].沈阳工业大学学报(社会科学版),2019,12(1):67-75.
[19] 曹君.对财产保险公司的经营风险管理研究 [J].金融经济,2018(10):48-49.