中国通过改革开放等政策提高了生产力水平,使经济得到了迅猛发展,一跃成为世界第二大经济体。与此同时,我国的环境也受到不同程度破坏。国家对这一问题非常重视,于2007年在政府收支分类科目中新增“节能环保”类财政支出,为环境保护工作提供财政保障;又于2014年4月24日通过了新修订的《环境保护法》。习近平总书记在党的十九大报告中再次强调,要重视生态文明、建设美丽中国。但是,发展经济与环境保护之间存在着一定矛盾,需要科学地权衡与解决。
地方政府承担着经济建设的责任,为地方经济发展、人民生活水平提升保驾护航、引领方向。同时,地方政府也是环境保护工作的主体,在治理经济建设活动带来的环境污染问题方面有着不可推卸的管理责任。因此,地方政府面临着既要全面建成小康社会,又要保证环境污染可控、实现可持续发展的重大挑战。因而,考虑环境污染因素的各省市投入 产出经济效率测度以及关于绿色全要素生产率变化及其收敛情况的研究就显得尤为重要。这也对判定各省市能否实现环境保护与经济发展之间的平衡具有重要意义。
一、文献综述
目前,国内学者在环境经济效率与绿色全要素生产率研究领域进行了一些探索。在环境经济效率的测度上:林伯强等运用非径向方向距离函数的超效率DEA模型测度了中国地级以上城市的绿色经济效率,通过工具变量法解决经济集聚与绿色经济效率之间的内生性问题,并进一步探究了经济集聚影响绿色经济效率的机制,认为经济集聚对绿色经济效率存在先促进后抑制的作用[1]。卓锦新等运用窗口DEA-SBM 模型测算了我国内地30个省、自治区、直辖市2003—2015年的生态经济效率,探讨了内部视角对生态经济效率的影响[2]。周杰文等采用超效率SBM 模型分析了2000—2017年“一带一路”沿线省份的绿色经济效率,并运用Tobit模型分析了影响因素,结果表明在南部和东北部的沿线省份绿色经济效率较高,地理因素与产业类型是造成绿色经济效率差异的主要原因[3]。张静等研究了汉江生态经济带11个城市2003—2015年的城市效率,其中考虑了生态环境成本问题[4]。在绿色全要素生产率的研究方面:许标文等基于稳健型整体方向性距离函数和整体Luenberger绿色生产率指标,测算了我国31个省份2001—2016年畜牧业绿色全要素生产率变化情况,认为畜牧业应尽快从要素投入向注重环境改善方面转变[5]。胡晓琳选用混合径向的DEA-EBM 模型并结合Malmquist模型,测算了我国内地29个省份2002—2013年的环境效率及环境全要素生产率,并对其收敛性和影响因素进行了深入研究,认为省级环境全要素生产率差异不会自动消失[6]。
现有研究尚存在一些不足:一方面,各学者选取的投入产出指标过于简单,且选取时随意性较大,不能全面反映环境经济实际状况,特别是在选取污染指标时往往采用总量而不是与各省地域面积相应的相对量,所以无法有效反映真实污染情况。另一方面,大部分文献选择传统的SBM 模型,这种非径向模型并不完全符合环境经济效率测度的需要,因为有些投入及产出指标需要等比例地扩大或缩减,而有些则不需要。另外,有些文献还存在指标选取过多等对DEA模型运用不够规范的问题。本文在规避这些问题的同时,采用新的视角,选取就业人数、资本存量、生产用电量、环保财政支出作为投入指标,将人均GDP及经过地域面积相对化处理后的各种污染物排放量作为产出指标,运用DEA-Hybrid模型及相邻前沿交叉参比Malmquist模型对中国内地2011—2017年30个省、自治区、直辖市的环境经济效率、绿色全要素生产率变化及其收敛性进行实证分析。
二、研究方法与数据选择
1.超效率Hybrid模型
传统的CCR或BCC模型是一种径向模型,即各项投入和产出的缩减或扩大必须是等比例的,这也是“径向”一词的含义。SBM 模型则可以将松弛变量问题融入对无效率的测量中,且可将非期望产出直接融入模型并设置为强可处置性,即某一投入或产出可以单独调整而不必要和其他指标一起调整。所以两类模型各有特点。但在现实生产中,并非所有投入或产出都可等比例改进或都是单独改进的,所以一种综合上述两类模型的混合距离函数模型应运而生,即Hybrid模型。Hybrid模型可以将投入和产出分为径向类指标和非径向类指标,综合了径向模型与SBM 模型的特点:如果所有指标均为径向的,则Hybrid模型等同于径向模型;如果所有指标均为非径向的,则Hybrid模型等同于SBM 模型。本文选取的投入指标中,劳动投入、资本投入、电力投入这3种生产要素投入一般是等比例存在的,但环保支出的投入就不必随着其他3种指标等比例改变;在产出指标中,各种污染物排放量指标一般是等比例产出的,但人均GDP这一产出指标就不必随其他污染指标等比例产出。所以,从本文选取指标的特质来看,Hybrid模型这种混合距离函数模型比较适合处理此类投入产出指标,比单纯的径向模型或SBM 模型更有优势。
超效率模型本质上是一种区分有效决策单元(DMU)的计算思路,而不是一种具体的函数模型,所以超效率模型是与其他径向模型或距离函数模型结合来实现的。具体做法是,将某个有效DMU单独拿出,再将其与其余DMU所构成的前沿进行比较。如此该有效DMU的效率值一般会大于1,这样就可以对所有有效的DMU进行进一步的效率值区分。在规划式中,只需加上j≠k这样一个限制条件,即从参考集中剔除被评价的DMU k[7]。因此,与超效率模型相结合的规模报酬不变的Hybrid模型规划式的一般形式为
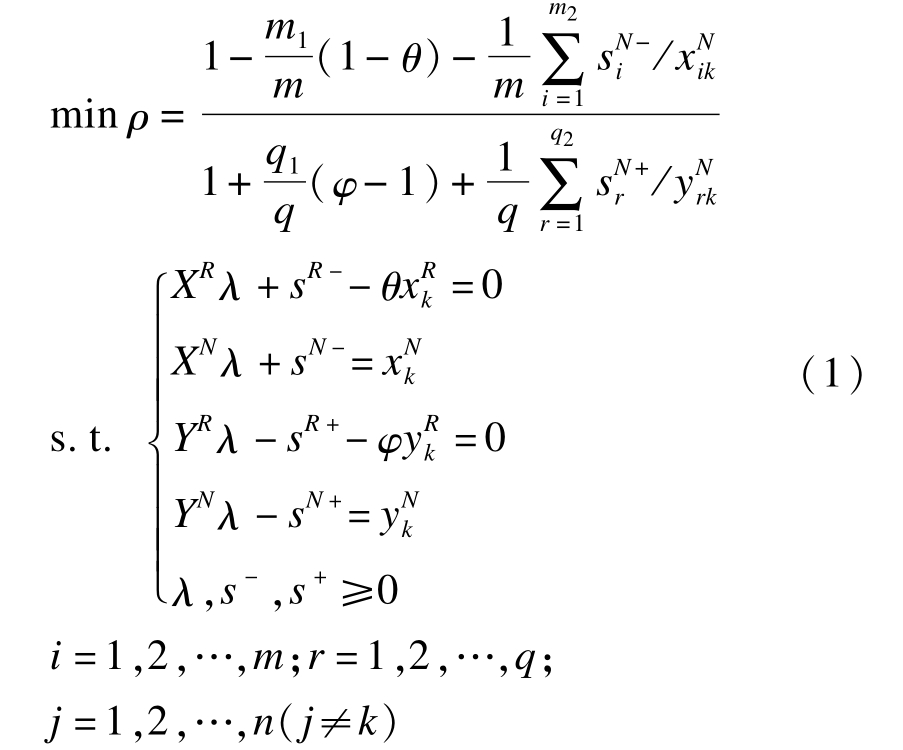
式中:上标N表示非径向指标、R表示径向指标;m为投入指标数量,其中m1为径向指标数量,m2为非径向指标数量;q为产出指标数量,其中q1为径向指标数量,q2为非径向指标数量[8];j表示第j个从参考集中剔除的需要测算超效率的DMU。
2.相邻前沿交叉参比Malmquist模型
Malmquist指数具体的计算思路大致可以理解为:将DMU tk与DMU t+1k 分别与不同的技术前沿参比,得出DMU t+1k 技术效率值与DMU tk技术效率值的比值,用以表示Malmquist指数[9]。目前,学界使用最广泛的Malmquist模型是传统的相邻前沿交叉参比(adjacent cross reference)模型,即分别参考两个前沿得出两个Malmquist指数后再取几何平均值,得出最终的Malmquist指数。除此模型之外,还有全局参比模型、固定参比模型、序列前沿交叉参比模型等其他类型的Malmquist模型。由于本文要对绿色全要素生产率的变化情况进行收敛性分析,需要Malmquist指数基于相邻两个年份的数据测算得出,因此采用传统的相邻前沿交叉参比模型最为合适[10]。从t时期到t+1时期的相邻前沿交叉参比模型为
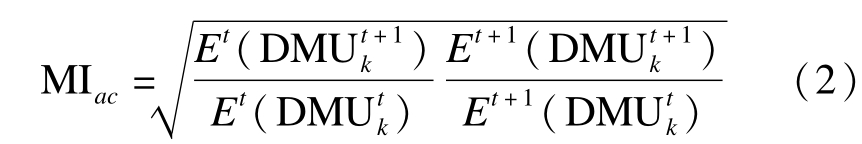
式中:Et+1(DMU tk)与Et(DMU tk)是DMU tk分别在t+1期和t期的技术效率值;Et+1(DMU t+1k )和Et(DMU t+1k )是DMU t+1k 分别在t+1期和t期的技术效率值。对两个时期的DMU进行交叉比较后取几何平均值,即所得的Malmquist指数。
3.条件β收敛检验
条件β收敛检验用于研究各经济体从长期来看是否存在动态演化趋势,以及各经济体之间的经济差距是否随时间推移而缩小。条件β收敛是相对于绝对β收敛而言的。绝对β收敛检验中,各经济体趋于收敛的是同一个稳定状态;而条件β收敛检验中,各经济体趋向于各自的稳定状态。所以条件β收敛假设不同经济体的基础条件和特征存在本质不同,承认发达经济体与欠发达经济体之间的差距始终存在[6]。因此,条件β收敛检验方法主要用于检验各经济体是否随时间推移而趋向各自的稳定状态。
4.数据选择
本文选择我国内地除西藏以外的30个省、自治区、直辖市作为研究对象,数据均来源于《中国统计年鉴》《中国环境统计年鉴》《中国能源统计年鉴》。因为国家统计局和环境保护部于2011年重新设置了部分污染指标的统计口径,且《中国统计年鉴》和《中国环境统计年鉴》公开的环境污染数据截止到2017年,所以本文选取的时间跨度为2011—2017年。测算环境经济效率本身就是在测算一个经济体考虑了环境因素后的投入产出效率及全要素生产率,因而在借鉴相关文献的指标选取后[11-13],本文在投入要素中选取城乡就业总人数(城乡非私营和私营个体就业人数总和)代表劳动投入,选取资本存量(通过永续存盘法计算得出)代表资本投入,选取生产用电量(用终端消费量减去生活消费量得出)代表资源投入,选取财政性环保支出额作为政府环保投入;在产出要素中选取人均GDP作为期望产出,代表经济产出成果;在非期望产出选取中,为了比较全面地反映实际污染情况,选取二氧化硫排放强度、氮氧化物排放强度、烟(粉)尘排放强度代表大气污染情况,选取化学需氧量排放强度、氨氮排放强度代表水体污染情况,选取一般工业固体废物产生强度代表土壤污染状况。为了客观准确地反映污染状况,对各污染指标都进行了地域面积的相对化处理,即除以各省市行政区域面积后得到各种污染物的排放强度指标。这种处理方法在环保部与财政部印发的环发〔2011〕18号文件中曾有提及。测算环境经济效率及绿色全要素生产率变化的投入与产出指标如表1所示。
表1 超效率Hybrid模型中各投入与产出指标

投入指标 产出指标城乡就业总人数/万人资本存量/亿元生产用电量/亿kW·h财政性环保支出额/亿元人均GDP/元·人-1二氧化硫排放强度/吨·(km2)-1氮氧化物排放强度/吨·(km2)-1烟(粉)尘排放强度/吨·(km2)-1化学需氧量排放强度/吨·(km2)-1氨氮排放强度/吨·(km2)-1一般工业固体废物产生强度/吨·(km2)-1
模型中,投入和产出指标共有11个,选取省、自治区、直辖市共30个,基本符合DMU数量大约为投入产出指标总数3倍这个DEA使用的一般原则[14]。
三、环境经济效率及绿色全要素生产率变化测算
1.各地方政府环境经济效率分析
本文主要测算综合技术效率,即假设各省份的生产状态为规模报酬不变。考虑到就业、招商引资等原因,通过降低投入而提高效率的思路并不符合实际情况,所以选择产出导向Hybrid模型,采用MaxDEA Ultra 6.7软件对2011—2017年我国内地30个省、自治区、直辖市的环境经济效率进行测算,结果如表2所示。
表2 (续)
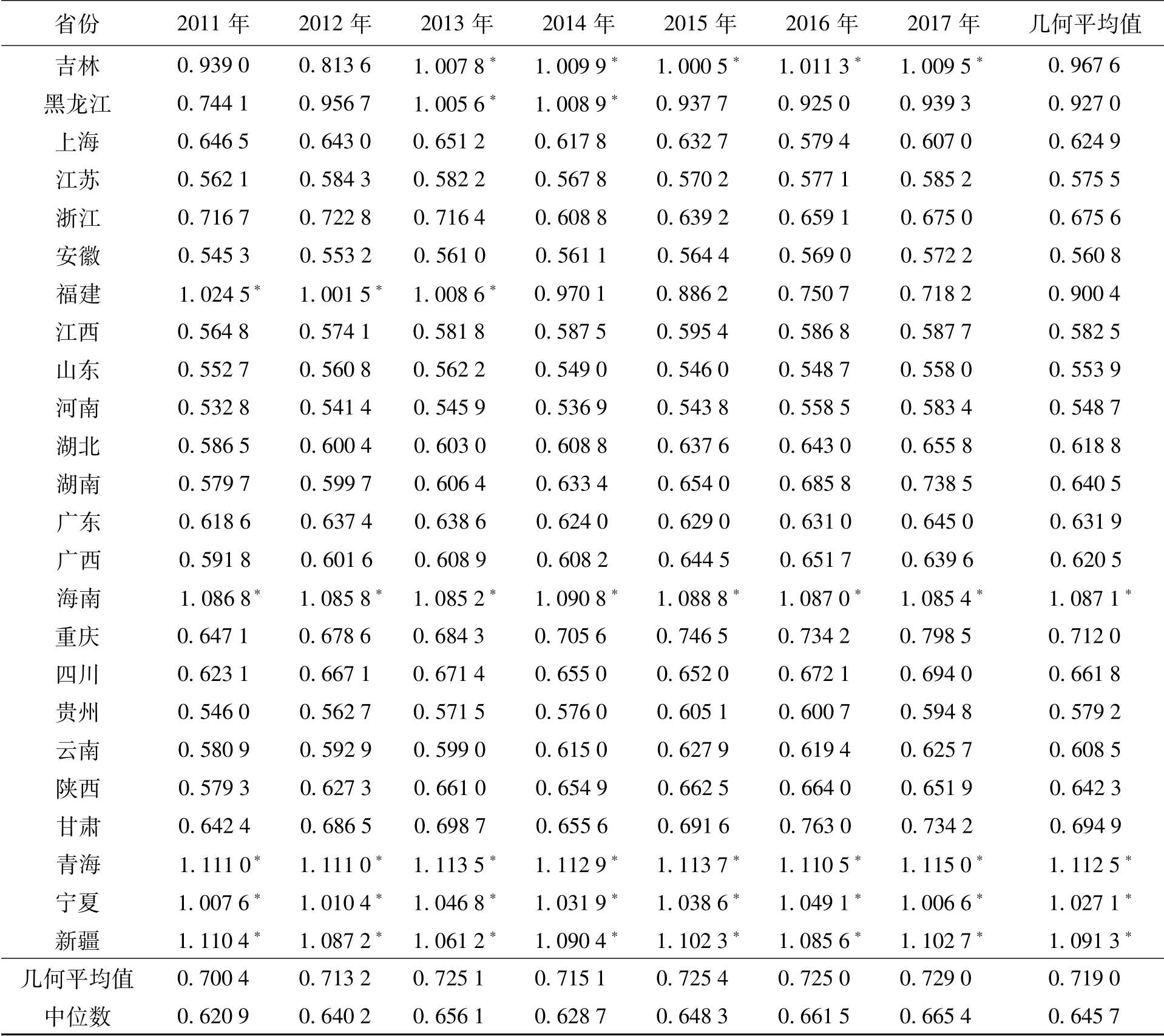
注:*表示DEA有效。
省份 2011年 2012年 2013年 2014年 2015年 2016年 2017年 几何平均值吉林 0.939 0 0.813 6 1.007 8*1.009 9*1.000 5*1.011 3*1.009 5*0.967 6黑龙江 0.744 1 0.956 7 1.005 6*1.008 9*0.937 7 0.925 0 0.939 3 0.927 0上海 0.646 5 0.643 0 0.651 2 0.617 8 0.632 7 0.579 4 0.607 0 0.624 9江苏 0.562 1 0.584 3 0.582 2 0.567 8 0.570 2 0.577 1 0.585 2 0.575 5浙江 0.716 7 0.722 8 0.716 4 0.608 8 0.639 2 0.659 1 0.675 0 0.675 6安徽 0.545 3 0.553 2 0.561 0 0.561 1 0.564 4 0.569 0 0.572 2 0.560 8福建 1.024 5*1.001 5* 1.008 6*0.970 1 0.886 2 0.750 7 0.718 2 0.900 4江西 0.564 8 0.574 1 0.581 8 0.587 5 0.595 4 0.586 8 0.587 7 0.582 5山东 0.552 7 0.560 8 0.562 2 0.549 0 0.546 0 0.548 7 0.558 0 0.553 9河南 0.532 8 0.541 4 0.545 9 0.536 9 0.543 8 0.558 5 0.583 4 0.548 7湖北 0.586 5 0.600 4 0.603 0 0.608 8 0.637 6 0.643 0 0.655 8 0.618 8湖南 0.579 7 0.599 7 0.606 4 0.633 4 0.654 0 0.685 8 0.738 5 0.640 5广东 0.618 6 0.637 4 0.638 6 0.624 0 0.629 0 0.631 0 0.645 0 0.631 9广西 0.591 8 0.601 6 0.608 9 0.608 2 0.644 5 0.651 7 0.639 6 0.620 5海南 1.086 8*1.085 8* 1.085 2*1.090 8*1.088 8*1.087 0*1.085 4* 1.087 1*重庆 0.647 1 0.678 6 0.684 3 0.705 6 0.746 5 0.734 2 0.798 5 0.712 0四川 0.623 1 0.667 1 0.671 4 0.655 0 0.652 0 0.672 1 0.694 0 0.661 8贵州 0.546 0 0.562 7 0.571 5 0.576 0 0.605 1 0.600 7 0.594 8 0.579 2云南 0.580 9 0.592 9 0.599 0 0.615 0 0.627 9 0.619 4 0.625 7 0.608 5陕西 0.579 3 0.627 3 0.661 0 0.654 9 0.662 5 0.664 0 0.651 9 0.642 3甘肃 0.642 4 0.686 5 0.698 7 0.655 6 0.691 6 0.763 0 0.734 2 0.694 9青海 1.111 0*1.111 0* 1.113 5*1.112 9*1.113 7*1.110 5*1.115 0* 1.112 5*宁夏 1.007 6*1.010 4* 1.046 8*1.031 9*1.038 6*1.049 1*1.006 6* 1.027 1*新疆 1.110 4*1.087 2* 1.061 2*1.090 4*1.102 3*1.085 6*1.102 7* 1.091 3*几何平均值 0.700 4 0.713 2 0.725 1 0.715 1 0.725 4 0.725 0 0.7 29 0 0.719 0中位数 0.620 9 0.640 2 0.656 1 0.628 7 0.648 3 0.661 5 0.6 65 4 0.645 7
表2 2011—2017年相关省份环境经济效率值
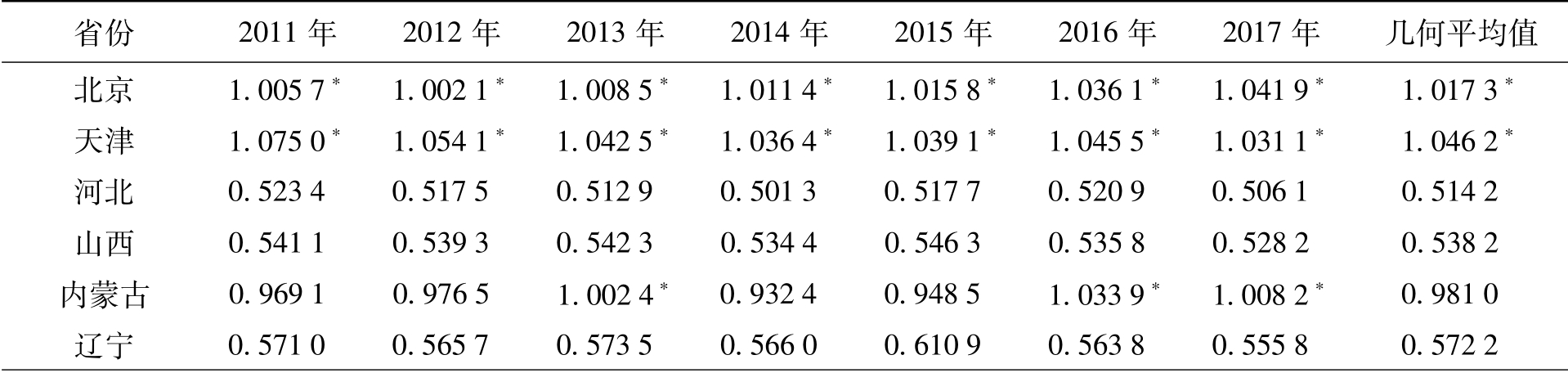
省份 2011年 2012年 2013年 2014年 2015年 2016年 2017年 几何平均值北京 1.005 7*1.002 1*1.008 5*1.011 4*1.015 8*1.036 1*1.041 9* 1.017 3*天津 1.075 0*1.054 1*1.042 5*1.036 4*1.039 1*1.045 5*1.031 1* 1.046 2*河北 0.523 4 0.517 5 0.512 9 0.501 3 0.517 7 0.520 9 0.506 1 0.514 2山西 0.541 1 0.539 3 0.542 3 0.534 4 0.546 3 0.535 8 0.528 2 0.538 2内蒙古 0.969 1 0.976 5 1.002 4*0.932 4 0.948 5 1.033 9*1.008 2* 0.981 0辽宁 0.571 0 0.565 7 0.573 5 0.566 0 0.610 9 0.563 8 0.5 55 8 0.572 2
从表2的结果中可以看出:
首先,2011—2017年间相关省份的环境经济效率大部分为DEA无效状态。7年中一直处于DEA有效状态的省份有6个:北京、天津、海南、青海、宁夏、新疆,部分年份为DEA有效的省份有4个:内蒙古(3年)、吉林(5年)、黑龙江(2年)、福建(3年),其余省份在7年中均属DEA无效。从未处于技术前沿面的省份占比达到66.7%,即7年中全国有2/3的省份长期处于环境经济无效率状态,要么是经济发展不够理想、人均GDP不够高,要么是环境污染治理效果不够理想、污染物排放强度较高。这些DEA无效率省份未能实现经济发展与环境保护的平衡,在经济发展的同时未能高效控制环境污染。
其次,各省份的效率值差距较大。从每年各省份效率值的中位数可以看出,7年来中位数均处在0.6这个数量级,最低为2011年的0.620 9,最高为2017年的0.665 4。如果将0.7作为上限,那么每年至少有一半省份的环境经济效率值在0.7以下,距离各年的生产技术前沿较远。从各省份7年的几何平均值看,最高的3个是青海(1.112 5)、新疆(1.091 3)和海南(1.087 1),而最低的3个是河北(0.514 2)、山西(0.538 2)和河南(0.548 7)。纵观所有省份7年的几何平均值,处于0.7以下的有19个,占63.3%。福建的几何平均值为0.900 4,排在其后的重庆市陡降至0.712 0,可见各省份环境经济效率值差距较大,存在比较明显的两极分化情况。
最后,从7年间的环境经济效率变动看,全国整体几何平均值从2011年的0.700 4逐步升高到2017年的0.729 0,增长了4.08%,说明我国环境经济效率总体上是在提高的。但是各省份的环境经济效率变化趋势则出现分化:效率值呈上升趋势的有北京、内蒙古、吉林、安徽、江西、河南、湖北、湖南、广东、广西、重庆、四川、贵州、云南、甘肃15个省份,其中北京、吉林、湖南、重庆上升趋势较为明显;效率值呈下降趋势的有天津、河北、山西、上海、浙江、福建6个省份,其中天津、福建下降趋势较为明显;效率值整体稳定略有波动的有辽宁、江苏、山东、海南、陕西、青海、新疆7个省份;效率值呈先升后降趋势的有黑龙江、宁夏2个省市。可以看出,效率值呈上升趋势的省份占50%,如果再加上稳定波动的7个省份以及天津、宁夏两个虽未上升但一直处于生产前沿面的省份,可以说全国各省份中效率值上升与稳定占比达到80%。这表明,自2011年起我国环境经济效率整体上越来越高,在保证经济增长、提高人民生活水平的同时,能够将环境污染问题控制在一个可接受的范围内,基本实现了经济发展与环境保护的相对平衡。
综合以上分析可以发现一些问题:经济发达、人口密集或工业主导的省份未必存在环境经济效率低下的现象,而经济发展水平有限、工业比重较低或以旅游业为支柱产业的省份环境经济效率也未必高。例如:北京、天津、上海、江苏、浙江、山东、广东、重庆、四川等省份近些年经济发展较快,往往会带来环境污染的压力,其中大部分省份效率均值低于0.7,但北京(均值1.017 3)和天津(均值1.046 2)却一直处于生产技术前沿面上。如果说青海、宁夏、新疆处于生产技术前沿面上是因为其经济欠发达使得污染压力较小,那么同样经济欠发达的云南、贵州、广西等省份的效率均值却均在0.6左右徘徊。同处于东北老工业基地的辽宁、吉林、黑龙江环境经济效率差异显著,吉林与黑龙江均值都在0.9以上,且吉林的效率值逐年攀升,7年中有5年处于生产技术前沿面上,黑龙江也有2年处于前沿面上,而辽宁的效率均值只有0.572 2,且无明显进展。因此,发展经济带来的环境污染压力虽然会对一个省份的环境经济效率产生一定影响,但并不是决定环境经济效率的关键要素。环境经济效率与各省份劳动、资本、资源等生产要素的投入比例,协同作用的发挥,生产技术与管理能力,环保支出使用过程,环境治理手段与监察力度,各企业配合情况等都有着密切的关系。运用DEA模型测算综合技术效率的过程,本身就是在寻找将这些因素结合起来运用得最好的省份,是在测算一个决策单元使用投入创造产出的整体绩效[15],这也是数据包络分析的价值所在。所以,处于生产前沿面DEA有效的省份就是在全国30个省、自治区、直辖市中经济发展与环境治理工作综合表现最好的省份,而DEA无效的省份就是尚有欠缺和不足的省份——或者经济发展不充分,或者环境污染控制成效低,或者兼而有之。
2.各省份绿色全要素生产率变化分析
上文中测算的综合技术效率是一个决策单元(DMU)在第t期中相对于技术前沿面的距离,而全要素生产率是一个DMU在第t期的生产力水平。因为研究过程中加入了环境污染指标,所以此生产率称之为绿色全要素生产率,旨在表明在考虑环境污染的情况下各省份的生产力水平。相邻前沿交叉参比Malmquist指数可以衡量一个DMU相邻两个时期内绿色全要素生产率的变化情况:MI ac大于1说明在连续的两个时期中该DMU的绿色全要素生产率提高,小于1说明生产率下降,等于1说明没有变化。
选用MaxDEA Ultra 6.7软件,基于超效率Hybrid模型并结合相邻前沿交叉参比Malmquist模型,测算2011—2017年相关省份绿色全要素生产率变化情况,结果如表3所示。
表3 (续)
省份 2011—2012年 2012—2013年 2013—2014年 2014—2015年 2015—2016年 2016—2017年 几何平均值安徽 1.007 75 1.009 00 1.000 44 1.000 55 1.020 47 1.01 2 76 1.008 47福建 0.993 42 0.975 52 1.068 73 0.807 07 1.025 42 0.981 05 0.971 53江西 1.010 05 1.007 10 1.011 83 1.005 53 1.000 52 1.010 45 1.007 57山东 1.005 78 1.002 52 0.978 87 0.996 78 1.024 18 1.022 90 1.005 05河南 1.007 73 1.005 92 0.990 32 1.009 06 1.039 91 1.052 25 1.017 31湖北 1.011 56 1.007 63 1.008 19 1.030 71 1.034 84 1.037 40 1.021 64湖南 1.022 15 1.011 52 1.043 17 1.021 99 1.111 67 1.093 77 1.050 02广东 1.007 94 1.005 55 0.980 53 1.049 56 1.042 25 1.025 66 1.018 31广西 1.005 67 1.016 30 0.997 66 1.041 30 1.037 47 0.997 05 1.015 75海南 1.001 85 1.000 35 1.001 55 0.994 50 1.006 49 0.999 22 1.000 65重庆 1.073 31 1.026 16 1.038 48 1.065 81 1.162 74 1.088 66 1.074 98四川 1.059 19 1.017 23 0.961 23 1.021 90 1.104 38 1.056 70 1.035 82贵州 1.018 96 1.013 62 1.005 70 1.031 71 1.010 72 0.998 87 1.013 21云南 1.015 34 1.014 77 1.018 57 1.028 97 1.048 12 1.024 13 1.024 92陕西 1.027 67 1.027 28 0.994 60 0.993 25 1.042 62 0.998 53 1.013 81甘肃 1.047 77 1.026 97 0.936 01 1.019 45 1.140 29 0.986 32 1.024 28青海 0.999 13 1.000 82 0.999 32 1.000 42 1.005 06 0.999 33 1.000 68宁夏 1.009 35 1.016 14 1.003 04 0.984 52 1.037 61 0.977 70 1.004 53新疆 0.983 12 0.995 28 1.019 82 1.002 93 0.994 32 1.001 93 0.999 50几何平均值 1.020 00 1.016 77 0.997 19 1.001 72 1.059 93 1.01 7 33 1.018 62
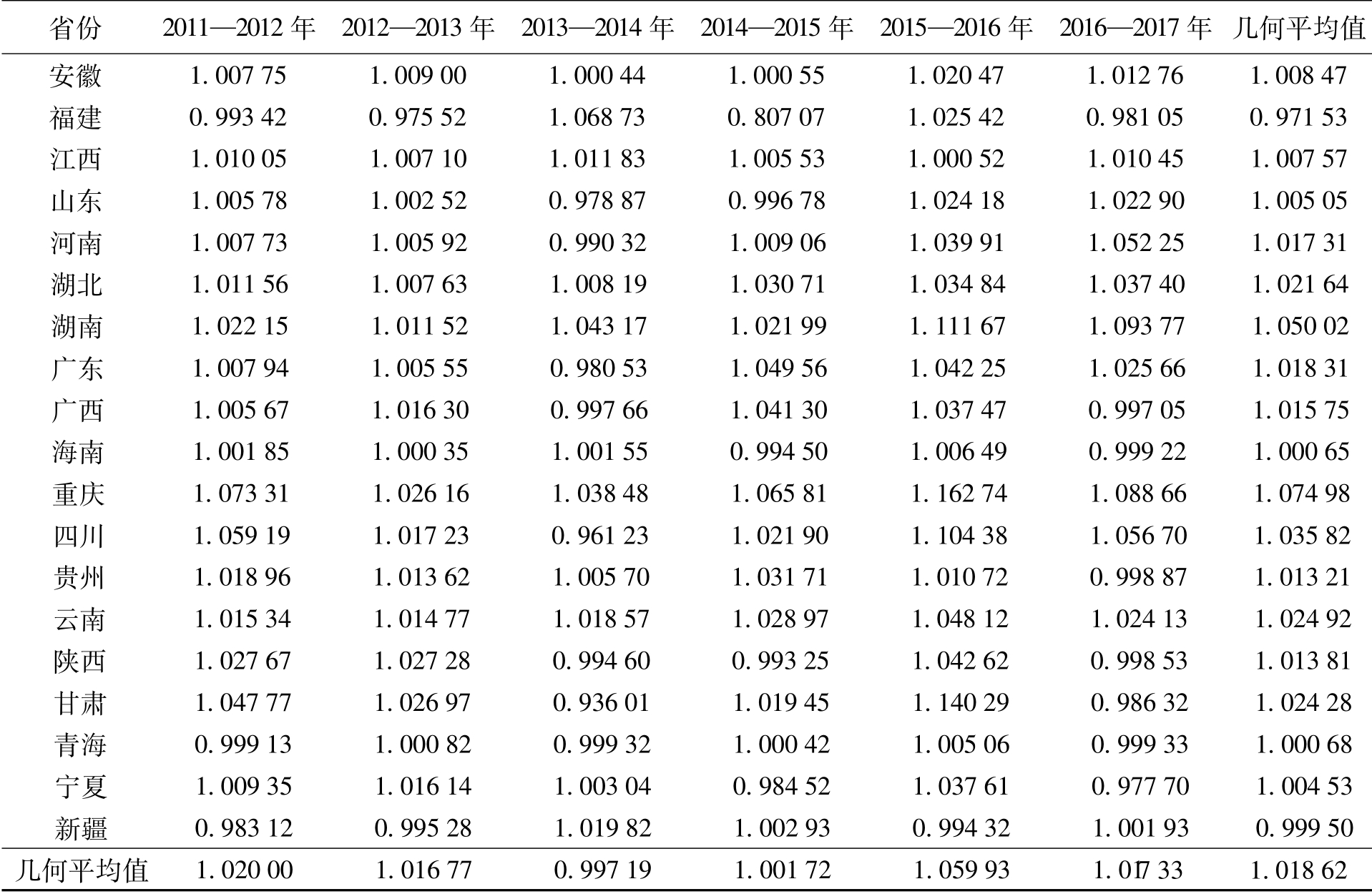
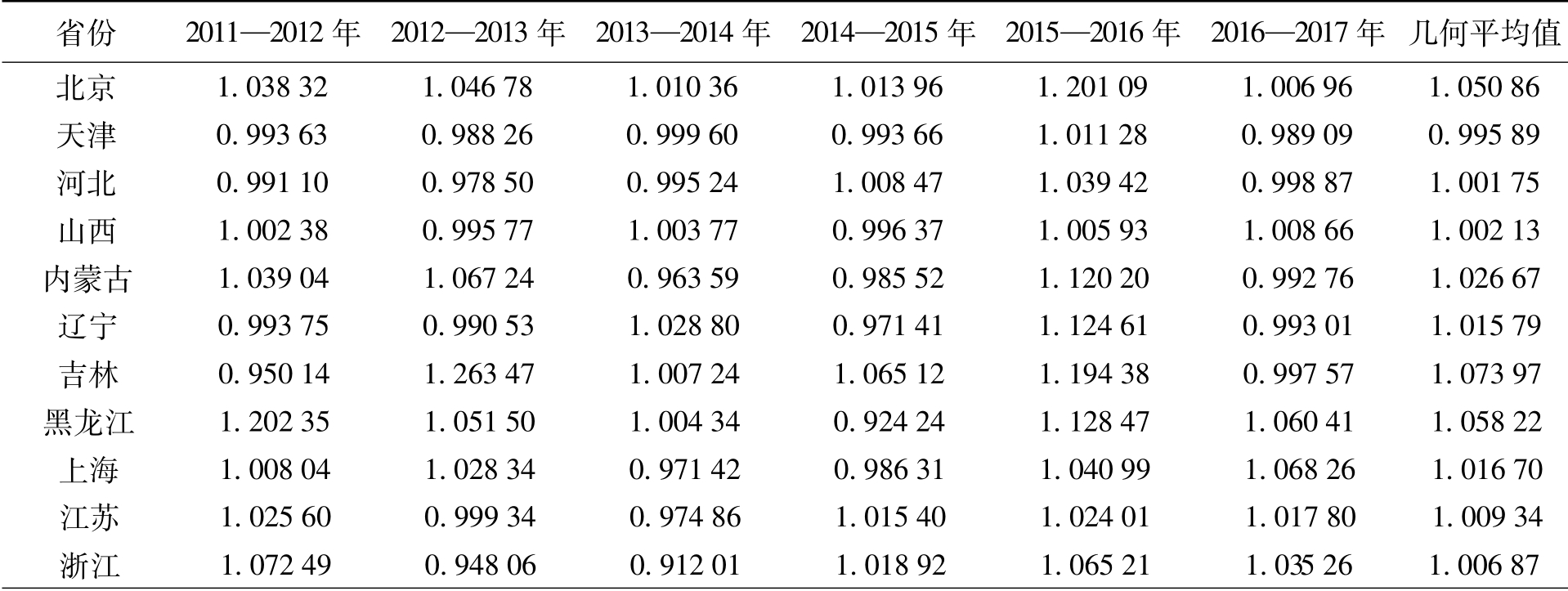
表3 2011—2017年相关省份绿色全要素生产率变化情况
省份 2011—2012年 2012—2013年 2013—2014年 2014—2015年 2015—2016年 2016—2017年 几何平均值北京 1.038 32 1.046 78 1.010 36 1.013 96 1.201 09 1.00 6 96 1.050 86天津 0.993 63 0.988 26 0.999 60 0.993 66 1.011 28 0.989 09 0.995 89河北 0.991 10 0.978 50 0.995 24 1.008 47 1.039 42 0.998 87 1.001 75山西 1.002 38 0.995 77 1.003 77 0.996 37 1.005 93 1.008 66 1.002 13内蒙古 1.039 04 1.067 24 0.963 59 0.985 52 1.120 20 0.992 76 1.026 67辽宁 0.993 75 0.990 53 1.028 80 0.971 41 1.124 61 0.993 01 1.015 79吉林 0.950 14 1.263 47 1.007 24 1.065 12 1.194 38 0.997 57 1.073 97黑龙江 1.202 35 1.051 50 1.004 34 0.924 24 1.128 47 1.060 41 1.058 22上海 1.008 04 1.028 34 0.971 42 0.986 31 1.040 99 1.068 26 1.016 70江苏 1.025 60 0.999 34 0.974 86 1.015 40 1.024 01 1.017 80 1.009 34浙江 1.072 49 0.948 06 0.912 01 1.018 92 1.065 21 1.03 5 26 1.006 87
从表3中可以看出,7年间除2013—2014年各省份均值为0.997 19之外,其余5个时间跨度均值都大于1,且总体上6个时间跨度的几何平均值为1.018 62,表明全国范围内绿色全要素生产率变化呈现不断上升的趋势,7年间平均提高了1.862%。从各省份情况看,北京、安徽、江西、湖北、湖南、重庆、云南7个省份在各时间段数值均大于1,说明这些省份绿色全要素生产率一直在提高。其他省份或多或少有部分时间段的绿色全要素生产率是下降的,且没有一直小于1的情况。从几何平均值看,30个省份中只有天津(0.995 89)、福建(0.971 53)、新疆(0.999 50)小于1,说明90%的省份在7年中绿色全要素生产率整体有所提高。需要指出的是,北京作为我国政治、经济和文化中心,在经济发展和环境保护的平衡方面发挥了先锋作用,其绿色全要素生产率连年提高、环境经济效率连年处于全国前列。虽然北京作为首都具有行政区域的特殊性,在经济发展和环境治理方面力度会更大,但也不能否定北京在实现发展与环保平衡过程中的优秀表现。相比之下,天津的表现不甚理想,虽然环境经济效率每年都处于全国前列,但效率值却逐年下降,绿色全要素生产率几乎也是逐年下降。这可能是由于相对其他省份而言,天津的生产投入存在逐年冗余,或污染指标下降速度稍慢,进而表现为经济发展与环境保护逐渐失衡的状态。新疆的环境经济效率连年处于全国前列,但平均绿色全要素生产率出现下降,表明生产技术前沿面在新疆这个观测点上出现了后移。对于相关省份整体绿色全要素生产率大于1的结果,结合前文对环境经济效率分析可以看出,绿色全要素生产率的普遍提高主要来自于生产技术前沿面的前移,而非技术效率的提高。
3.各省份绿色全要素生产率收敛性分析
由于各个省份当前存在着经济基础与环境状况的天然差异,且短时间内这种差异不会消失,因此本文采用条件β收敛检验方法分析2011—2017年相关省份绿色全要素生产率指数的收敛情况。前文测算的MI ac值是绿色全要素生产率的变化率,通常的做法是将某一时间跨度的MI值定义为跨度末期年份的全要素生产率指数。本文即采取这种做法,赋予2011年各省份绿色全要素生产率指数为1,据此得到2011—2017年绿色全要素生产率指数的一组面板数据。对于条件β收敛的检验方法,胡晓琳以先验理论为依据,采用构建条件β收敛回归模型的方法进行检验[6],公式为
式中,GTFP it为第i个省份第t期的绿色全要素生产率指数;GTFP i,t-1为第i个省份第t-1期的绿色全要素生产率指数;α为面板数据模型固定效应截距;β为模型的回归系数。
构建面板数据回归模型并使用Eviews 10.0软件进行回归测算,在Weights项中选择Crosssection Weights并同时选择PCSE方法,对模型进行广义最小二乘法估计,以解决可能存在的随机误差项不满足等方差的假设,并有效处理复杂的面板误差结构。模型估计结果如表4所示。
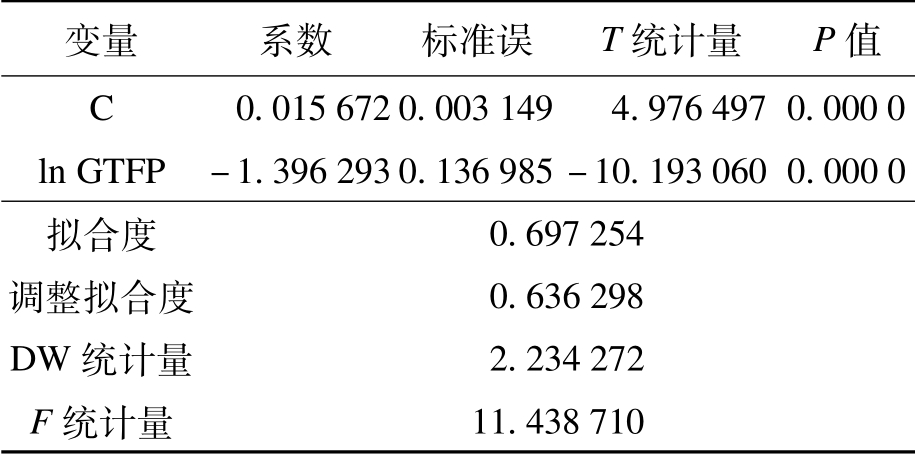
表4 条件β收敛回归模型估计结果
变量 系数 标准误 T统计量 P值C 0.015 6720.003 149 4.976 497 0.000 0 ln GTFP -1.396 293 0.136 985-10.193 060 0.000 0拟合度0.697 254调整拟合度 0.636 298 DW 统计量 2.234 272 F统计量11.438 710
在回归结果中,β估计值小于0,回归结果为-1.396 293且通过了1%的显著性检验,判定系数结果尚可,DW 值在2附近,回归结果良好。这说明从整体看,相关省份2011—2017年的绿色全要素生产率存在条件β收敛,表明其绿色全要素生产率存在向自身稳定状态收敛的趋势。
四、结论与建议
本文运用超效率Hybrid模型和相邻前沿交叉参比Malmquist模型测算了2011—2017年我国内地30个省、自治区、直辖市的环境经济效率及绿色全要素生产率变化情况,并利用条件β收敛方法检验了绿色全要素生产率的收敛性。在环境经济效率方面,7年中相关省份普遍处于DEA无效状态,各省市之间效率值差距较大,但从总体上看增长了4.08%,在经济发展与环境保护之间保持相对平衡方面存在向好的趋势。经济发达、人口密集或以工业主导的省份未必存在环境经济效率低下现象,而经济发展水平有限、工业比重较低或以旅游业为支柱产业的省份也未必具有较高的环境经济效率。在绿色全要素生产率变化方面,全国范围内呈现不断上升的趋势,7年间平均提高了1.862%,且相关省市的绿色全要素生产率存在向其自身稳定状态收敛的趋势。据此,本文提出如下建议:
(1)搭建信息共享平台,促进绿色发展经验交流。DEA模型测算的是各DMU之间的相对效率值,是以“最佳实践”的DMU为标杆进行比较得出的效率值。因此,DEA有效的省份就是在经济发展与环境保护达到相对平衡方面“表现最佳”的省份。在分析结果中,一些省份的环境经济效率值偏低或绿色全要素生产率下降,本质原因或者是经济发展不充分,或者是环境污染控制成效低,或者兼而有之。因此,“表现欠佳”的省份需要向“表现最佳”的省份学习成功的经验和方法,复制“最佳实践”路径,从而缩小与DEA有效省份的差距。北京作为我国的政治、经济与文化中心,产业众多、人口密集,无论是经济发展还是环境保护压力都比较大,但其连续7年处于DEA有效状态,这是同样发达的上海无可比拟的。虽然北京作为首都具有特殊性,一些工作的实施可能更有效率,但其实践经验依然值得借鉴。吉林处于东北老工业基地,经济发展情况并不理想,工业带来的环境污染压力较大,但其效率均值在0.9以上且逐年攀升,有5年处于生产技术前沿面上,因此其实践经验也非常值得借鉴。所以,各省份应构建信息交流共享平台,将促进经济发展与控制环境污染的经验和方法在全国范围内分享交流,从而提高全国经济发展与环境保护相平衡的实践水平。
(2)调整财税手段,加强政府的促进作用。一方面,各省份政府应重视对环保工作的财政支持,主要包括继续增加节能环保方面的财政投入、对环保技术研发的补贴、对环保领域投资企业的支持补贴、对高校和科研院所产学研结合的补贴、对企业使用清洁能源和提高能源利用率的投入补贴等[6]。这样的财政支持能够同时从经济发展、技术提升、环境保护等多个角度发挥促进作用。另一方面,在上述领域除配合财政支出的税收减免政策之外,还应充分发挥《中华人民共和国环境保护税法》的作用,从法律维度配合政府的财税政策,形成促进与维护绿色经济发展的公权制度体系。
(3)完善环保监督机制,提高环保单位业务能力。环保监察是环境保护工作的重中之重,在保证环保部门财政预算充足合理的前提下,环保监督部门应严格遵守环保审批制度,加强环保审查和验收力度,配合司法机关加强随机调访和夜间执法力度,调动居民自发监督的积极性,以及加强对这些手段的法律支撑。同时,及时归纳、总结、交流环保工作中的经验与心得体会,全面提升环保单位的组织管理能力和工作人员的个人工作能力,从而有效控制环境污染,实现经济发展与环境保护的平衡。
[1]林伯强,谭睿鹏.中国经济集聚与绿色经济效率[J].经济研究,2019,54(2):119-132.
[2]卓锦新,曹烨,邱国玉.我国区域资源环境与经济协调特征研究——基于窗口SBM 模型[J].管理现代化,2018,38(2):17-20.
[3]周杰文,赵月,杨阳.“一带一路”沿线省份绿色经济效率时空差异研究[J].统计与决策,2020,36(22):100-103.
[4]张静,丁斐.基于DEA-ESDA的汉江生态经济带城市效率研究[J].湖北社会科学,2017(9):52-59.
[5]许标文,沈智扬,林国华.中国畜牧业绿色全要素生产率演变及区域差异研究[J].中国生态农业学报(中英文),2019,27(4):613-622.
[6]胡晓琳.中国省际环境全要素生产率测算、收敛及其影响因素研究[D].南昌:江西财经大学,2016:82-84.
[7]Andersen P,Petersen N C.A procedure for ranking efficient units in data envelopment analysis[J].Management Science,1993,39(10):1261-1264.
[8]赵红,刘健欣,闫妍.基于DEA方法的线上零售类电子商务企业经营效率评价[J].沈阳工业大学学报(社会科学版),2020,13(6):534-539.
[9]李伯棠,李永生,周海英,等.中国省际环境全要素生产率及空间溢出效应研究[J].统计与决策,2021,37(4):10-14.
[10]吴洋.辽宁省地方政府财政性环保支出生产率变化分析[J].沈阳师范大学学报(社会科学版),2019,43(5):41-46.
[11]陈黎明,王俊昊,赵婉茹,等.中国区域绿色全要素生产率的影响因素及其空间特征[J].财经理论与实践,2020,41(4):122-132.
[12]刘淑茹,贾箫扬,党继强.中国工业绿色全要素生产率测度及影响因素研究[J].生态经济,2020,36(11):46-53.
[13]余奕杉,卫平.中国城市绿色全要素生产率测度研究[J].生态经济,2021,37(3):43-52.
[14]Cooper W W,Seiford L M,Tone K.Data envelopment analysis:a comprehensive text with models,applications,references and DEA-solver software[EB/OL].[2021-03-02].https://www.oalib.com/references/8020421.
[15]Zhu J.数据包络分析——让数据自己说话[M].公彦德,李想,译.北京:科学出版社,2016:51.