随着电子商务的快速发展,在线购物已成为顾客(本文指终端消费者)的重要购物方式之一。据统计,2020年“双11”全阶段天猫平台成交额4 982亿元,同比增长26%,预计未来仍将持续高速增长。然而,高交易额的背后也存在着交易距离远、产品性能与顾客需求不匹配等问题,导致顾客退货率居高不下。Grimaldi的分析数据显示,线上顾客退货率可达18%~35%,比传统的线下模式高出2~4倍[1]。高退货率严重影响商家收益,现实中在线商家普遍设置退回产品不得影响二次销售的门槛来降低退货损害,由此引发了大量可二次销售产品的退货策略问题。目前,关于无理由退货策略的理论研究大多假设顾客退回产品不再正价销售,这与现实情况并不相符。因此,本文放宽上述假设,针对退回产品二次销售情形下的在线无理由退货策略展开研究。
一、文献回顾
无理由退货最早由Davis提出,认为它是零售商主动承担产品与顾客需求不一致风险而付出产品体验价值的一项服务[2]。无理由退货策略对商家收益具有“双刃剑”的作用:一方面,通过慷慨的无理由退货策略可以获得顾客信任、提高顾客效用,增加商家收益。如Akçay等的研究表明,无理由退货策略可以增加零售商的利润[3];熊中楷等指出,在线营销时无理由退货策略起到了高质量信号作用,可以有效提高产品定价,从而提高在线零售商的收益水平[4]。另一方面,慷慨的无理由退货策略会带来再处理成本、产品价值损害等问题,降低商家收益。如Davis等指出,无理由退货服务会引发顾客的道德危害行为(moral hazard),顾客购买产品仅仅为了获取其体验价值,体验期过后便会退回产品,导致商家收益的损害[2];毛可等同时考虑零售商的销售策略和产品定价决策,发现随着消费者满意度的上升零售商利润反而有可能降低[5];何啸源等结合实际情况研究在线零售商的最优退货策略,结果表明在线零售商的利润随着部分退款期限的延长呈先增后减再增的趋势[6];McWilliams利用双寡头垄断模型,证明了无理由退货策略更有利于低质量零售商,而会损害高质量零售商的收益[7]。从上述研究可以看出,如何设置最优的无理由退货策略来平衡这种“双刃剑”作用,对商家收益水平具有重要影响。
目前,很多学者对无理由退货策略的设置展开研究,并取得了较为丰富的成果。如:Hess等提出部分返款(partial refund)概念,即顾客退货时只能获得部分返款,并证明了部分返款可以合理降低顾客恶意退货现象[8-9]。随后,不少学者对部分返款型退货策略的价值和退货价格的确定展开了深入研究,如:Su基于报童模型对全额退款和部分退款两种策略进行比较,认为部分返款优于全额返款,最优退货价格应设置为产品残值[10];Hsiao等通过设置退货障碍成本的方法实现部分返款,并在产品需求随机条件下对Hassle-free和MBG两类退货策略展开了价值对比研究[11];孙军等将退货障碍具体化为退货运费,并详细研究了其承担问题[12]。近年来,随着顾客行为引入运营管理领域,不少学者认识到顾客行为对无理由退货策略的设置具有重要影响,如:郑春东等对退货运费险的作用机理进行探索性研究,发现退货运费险能够显著降低消费者的感知风险,提高信任水平[13];Giri等在多个制造商和一个零售商构成的供应链环境下,研究不允许退货和全额退款两类情形下最优的产品销售价格和库存策略[14];Su最早将顾客战略行为引入无理由退货策略中[10]。国内学者也在考虑顾客战略行为的基础上对无理由退货策略设置及其价值展开了丰富研究,如:李建斌等通过探讨质量风险与提供无理由退货的在线零售商利润的关系,认为在特定技术成本和退货损失下,无理由退货是中等质量水平在线零售商的最佳退货处理策略[15];曾诚等分析三种大规模定制产品退货策略,提出针对不同退货时点分段设定退款额的退货策略[16];杨道箭等构建全渠道运营RTS服务模型,并对RTS价值进行理论建模研究[17];吴红迪等研究权力失衡下占主导地位零售商与制造商的退货策略协调机制,分析零售商要求按照批发价退货和采用退货策略退货两种情况[18]。
二、模型描述及假设
上述研究均未考虑顾客退回产品二次销售情况,而现实中这些产品往往是允许二次销售的。本文放宽顾客退回产品不再正价销售的假设,研究退回产品二次正价销售时的无理由退货策略,并针对顾客对产品曾售信息是否知情具体分为隐藏和公开产品曾售信息两种情况进行分析[19-20]。
假设市场上存在单个商家对产品实行跨期销售,销售期分为全价销售期(entire period,EP)和打折销售期(salvage period,SP)。在EP期,商家以销售价格p正常销售产品,产品总库存量为q,商家为顾客提供部分返款型无理由退货服务,退货价格为r(r<p),并且顾客退回产品可以在当期以全价p二次销售,二次销售产品的处理成本为c0。EP期结束后进入SP期,商家以打折价格s(s≤c)销售剩余产品,假设所有产品均能够打折售出。商家的销售及决策过程如图1所示。

图1 商家销售及决策过程
假设市场上的顾客具有战略性,他们以自身收益最大化为原则来进行行为决策。顾客需求为随机变量D,其分布函数和概率密度函数分别为F(·)和f(·)。产品在顾客心中的价值为随机变量V,其分布函数和概率密度函数分别为G(·)和g(·)。当需求量小于库存(D≤q)时,顾客无理由退回产品不需要参与二次销售,每次买到的产品均是从未售出过的;当需求量大于库存(D>q)时,退回产品将二次销售以满足顾客需求。由于现实中商家普遍会通过较长的EP期来实现较高收益,本文在D>q条件下展开研究。根据二次销售是否对产品在顾客心中的价值产生影响,分为商家向顾客隐藏产品曾售信息和公开曾售信息两种情况进行讨论。
三、隐藏产品曾售信息时的无理由退货策略
在EP期,假设商家向顾客隐藏产品曾售信息,则顾客会将所有产品视为从未售出过,二次销售对产品在顾客心中的价值无影响,其预期效用与不允许二次销售时相同,仍为
Emax(v,r)-p
(1)
战略顾客以自身收益最大化为原则进行购买和退货决策,整理可得顾客的最大支付意愿(Maximum Willing Price,MWP)为pMWP=Emax(v,r)。商家为追求利润最大,将设定产品的全价销售价格为p=Emax(v,r)。在SP期,所有剩余产品均以打折价格s售出,此时主要销售顾客退回产品。
1. 二次销售1次
假设D>q1且顾客退回产品只二次销售1次,本文处理二次销售的研究思路是:将EP期逻辑上虚拟划分为初次销售期和二次销售期两个阶段,商家在初次销售期只销售从未售出过的产品,在二次销售期只销售顾客无理由退回的产品,二次销售价格仍为全价p1;这两个销售期均提供无理由退货服务,退货价格为r1。具体销售过程如图2所示。

图2 二次销售1次的销售过程
从图2中可以看出,为了区分产品真实的销售次数,将商家的销售过程逻辑上分为3个阶段:初次销售期、二次销售期和打折销售期。在现实中,初次销售期和二次销售期是重叠的,二者同时存在于EP期。在初次销售期,由于D>q1并且允许顾客退货,此阶段产品销量为q,顾客退回产品数量为G(r1)q1,并全部进入二次销售期再次销售;在二次销售期,产品销量为Emin[D-q1,G(r1)q1],其中顾客退回产品为G(r1)Emin[D-q1,G(r1)q1],二次销售产品的再处理成本为c0Emin[D-q1,G(r1)q1];在打折销售期,商家以打折价格s清仓处理所有剩余库存G(r1)Emin[D-q1,G(r1)q1]。由上可知,商家的预期收益为
[c-sG(r1)]q1
(2)
式中,E1=Emin[G(r1)q1,D-q1]。
通过式(2)可以得到
定理1 当允许顾客退回产品二次销售时,商家最优决策为
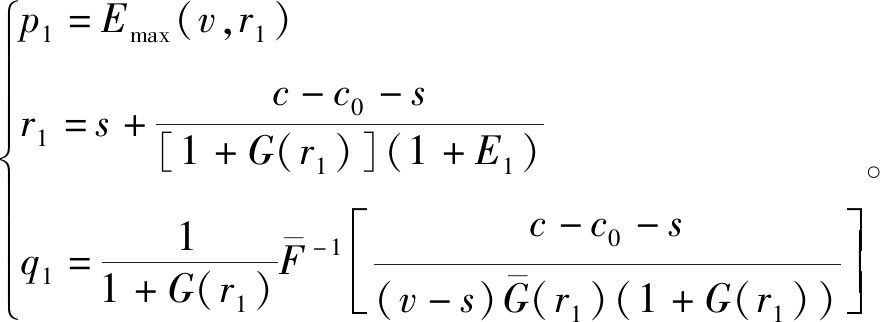
证明:令![]() 由式(2)对r1求导可得∂EΠ/
由式(2)对r1求导可得∂EΠ/![]() 整理可得最优退货价格
整理可得最优退货价格![]() 同理,由式(2)对q1求导可得∂EΠ/∂q1=v
同理,由式(2)对q1求导可得∂EΠ/∂q1=v![]() (r1)+[(v-s)
(r1)+[(v-s)![]() (r1)-
(r1)-![]() 整理可得
整理可得![]() 将
将![]() 代入r1,可得
代入r1,可得![]() 证毕。
证毕。
当顾客退回产品只二次销售1次时,商家最优销售价格、退货价格和库存量可以由定理1中的方程组求解得出。通过对定理1结论的分析可知,产品退货价格r1随着再处理成本c0的增加而降低,这与不允许二次销售时相同。当产品二次销售的总成本大于打折价格时(c-c0>s),产品退货价格高于不允许二次销售情形(r1>r0=s),否则r1≤r0=s。这说明只有当再处理成本较低时,商家在二次销售时才愿意更加慷慨地给予顾客退货补偿。定义E1=Emin(G(r1),D/q1-1)为顾客退回产品对顾客剩余需求(即上个销售期未被满足的顾客需求)的满足效用,则产品退货价格r1是该效用的减函数。这是由于二次销售期顾客退回产品将不能再以正价销售,因此商家降低退货价格,不希望顾客退货。为了便于计算,现实中商家可以利用以往的经验退货率Κ和供需比Γ来估算该效用值,即Emin(Κ,Γ-1)。当Γ-1≤Κ时,即顾客退回产品的二次销售预计能够满足全部顾客剩余需求时,产品供不应求程度Γ越高,则退货价格r1越低;当Γ>Κ时,即退回产品的二次销售不能满足顾客剩余需求时,退回产品能够被再次全部售出,产品退货价格不再与Γ相关,而与二次销售期的经验退货率呈负相关关系。对于销售价格,当隐藏产品曾售信息时,产品是否曾售对其在顾客心中的价值无影响,其销售价格p1仍是产品在顾客心中价值和对退货价格最大值的期望,且仍是退货价格r1的增函数,二者的正相关关系不受产品二次销售的影响。对于库存,定义![]() 为库存效用,表示产品二次销售1次时的实际销售次数,退回产品二次销售实际上会增加顾客购买产品的机会。由定理1可知,库存效用
为库存效用,表示产品二次销售1次时的实际销售次数,退回产品二次销售实际上会增加顾客购买产品的机会。由定理1可知,库存效用![]() 和真实库存q1均为退货价格的减函数,这与不允许二次销售时相同,且真实库存q1的这种递减效用更加明显。
和真实库存q1均为退货价格的减函数,这与不允许二次销售时相同,且真实库存q1的这种递减效用更加明显。
2. 二次销售n次
接下来将顾客退回产品的二次销售次数推广到n,同样利用虚拟销售期思路进行分析。其中,n为产品二次销售次数:n=0表示只销售未售出过产品,n=1表示只销售顾客退回1次的产品,依此类推,n=n表示销售顾客退回n次的产品。具体销售过程如图3所示。
从图3中可以看出,商家的销售过程逻辑上仍然可以划分为初次销售期、n个二次销售期和打折销售期。通过分析可知,初次销售期和二次销售次数为1,2,…,n-1时,每期期初需求均高于库存,净销量分别为qn,G(rn)qn,…,Gn-1(rn)qn;当销售次数为n时,顾客退回产品将不再二次销售而是直接进入打折销售期,净销量为![]() (rn)Emin[D-(1+G(rn)+…+Gn-1(rn))qn,Gn(rn)qn]。
(rn)Emin[D-(1+G(rn)+…+Gn-1(rn))qn,Gn(rn)qn]。

图3 二次销售n次的销售过程
全价销售期结束后,商家以价格s打折清仓所有剩余产品。假设所有产品均能售出,打折产品库存为G(rn)Emin[D-(1+G(rn)+…+Gn-1(rn))qn,Gn(rn)qn],则商家预期收益为
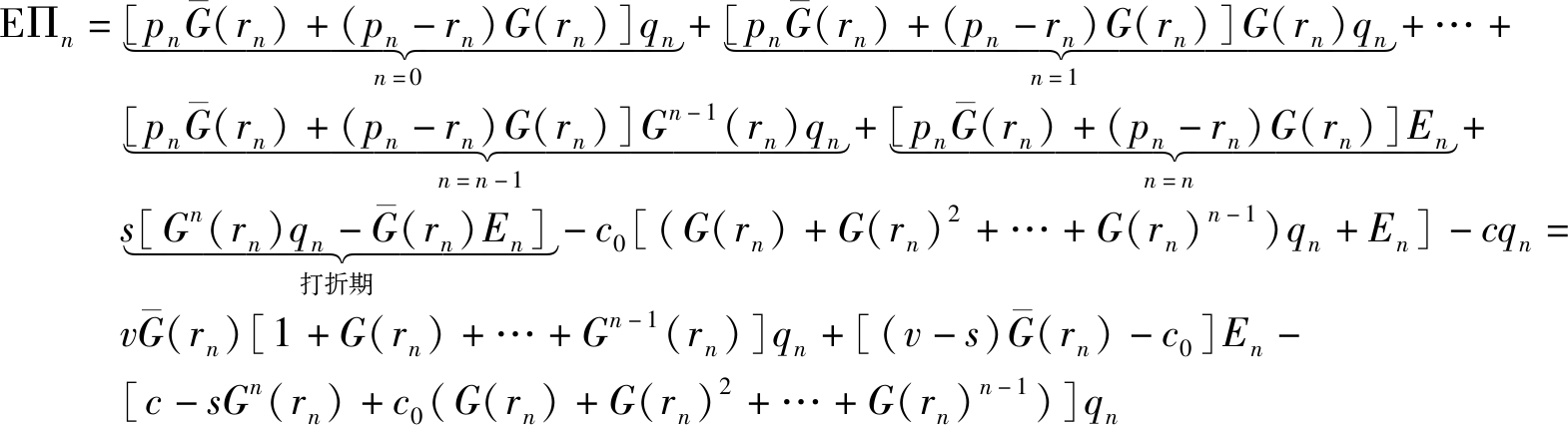
(3)
式中,记En=Emin[D-(1+G(rn)+…+Gn-1(rn))qn,Gn(rn)qn]。
由式(3)可得
定理2 当允许顾客退回产品二次销售n次时,商家的决策为
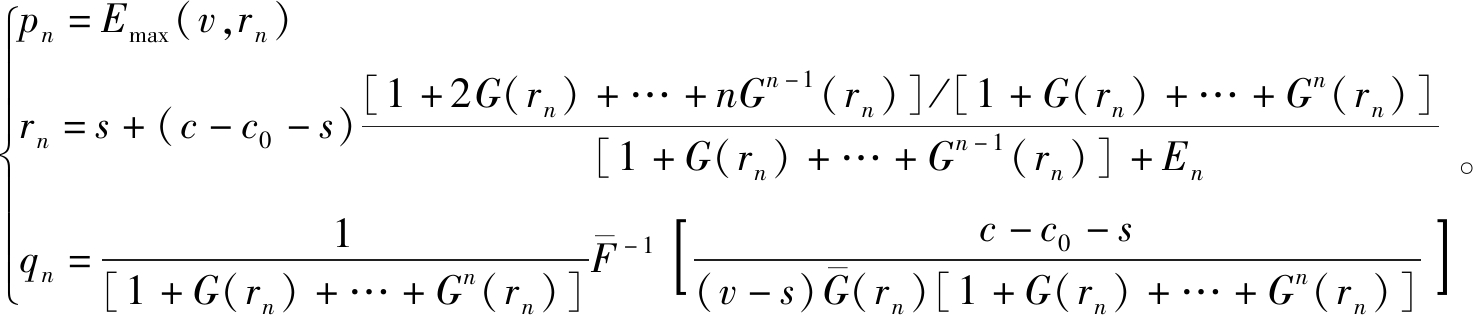
证明:令![]() 由式(3)对rn求导可得
由式(3)对rn求导可得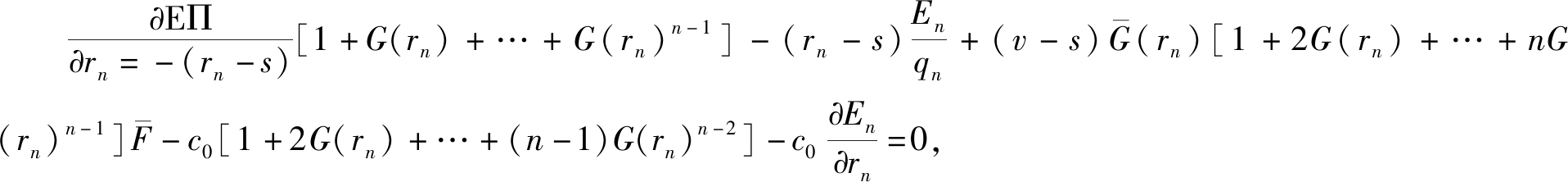 整理可得
整理可得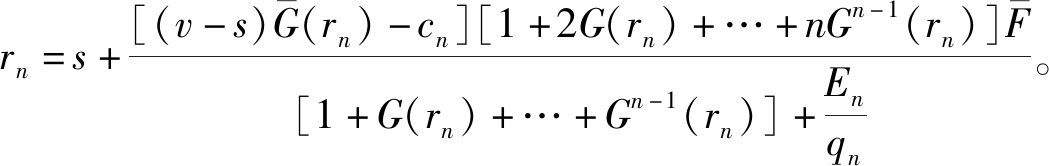 由式(3)对qn求导可得∂EΠ/∂qn=(v-s)
由式(3)对qn求导可得∂EΠ/∂qn=(v-s)![]() (rn)[1+G(rn)+…+G(rn)n]
(rn)[1+G(rn)+…+G(rn)n]![]() -(c-s)-c0[G(rn)+G(rn)2+…+
-(c-s)-c0[G(rn)+G(rn)2+…+![]() 整理可得
整理可得![]() 将
将![]() 代入rn可得
代入rn可得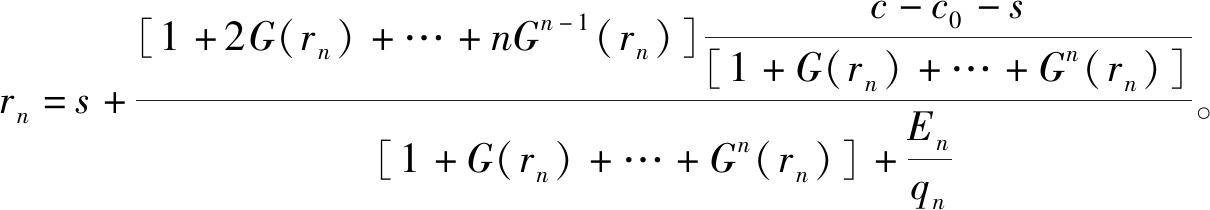 证毕。
证毕。
定理2给出了顾客退回产品被二次销售n次时产品的最优销售价格、退货价格和库存。其中,当n=1时,pn,rn,qn的结果与定理1相同。仍然定义二次销售对顾客剩余需求的满足效用为Emin[D/qn-(1+G(rn)+…+Gn-1(rn)),Gn(rn)],退货价格rn同样是该效用的减函数,这与二次销售1次时相同。当n变化时,rn是产品二次销售次数n的增函数,说明产品能被二次销售次数越多,则商家给予顾客的退货价格就越慷慨。产品的销售价格pn仍然与退货价格正相关,是二次销售次数n的增函数,这是由于二次销售次数使退货价格更加慷慨,从而增加了顾客效用。对于库存,同样令![]() 为库存效用,表示二次销售n次时的产品实际销售次数。与定理1相同,
为库存效用,表示二次销售n次时的产品实际销售次数。与定理1相同,![]() 亦是退货价格rn的减函数。当二次销售次数n变化时,
亦是退货价格rn的减函数。当二次销售次数n变化时,![]() 和qn随着n的增加反而降低,这是由于产品二次销售增加了同一产品对顾客需求满足的次数,产品的二次销售实际上起到了降低进货量的作用。
和qn随着n的增加反而降低,这是由于产品二次销售增加了同一产品对顾客需求满足的次数,产品的二次销售实际上起到了降低进货量的作用。
四、公开产品曾售信息时的无理由退货策略
现实中,顾客拿到产品后往往会根据包装等信息判断该产品是否曾经售出过,曾售特征会影响顾客对产品的感知价值。下文将对产品公开曾售信息(以上标m表示)时的退货策略进行研究。
假设商家公开产品曾售信息,令产品曾售对其在顾客心中价值损害为常数M,则曾售产品在顾客心中的价值为V-M。与销售全新产品不同,当![]() 时,顾客选择保留产品;否则
时,顾客选择保留产品;否则![]() 顾客选择退货。顾客购买全新和曾售产品的比例分别为
顾客选择退货。顾客购买全新和曾售产品的比例分别为![]() 和
和![]() 此时顾客购买产品的预期效用为
此时顾客购买产品的预期效用为
![]()
(4)
式中:
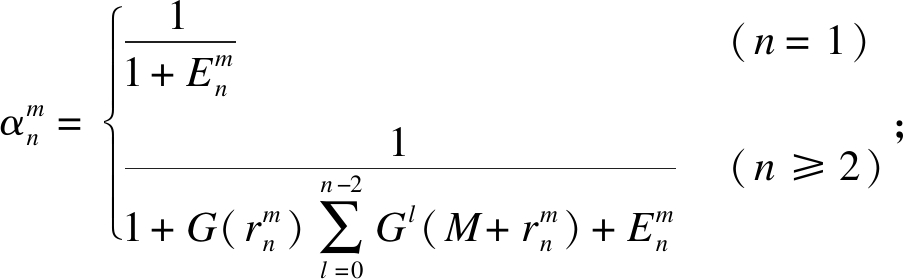
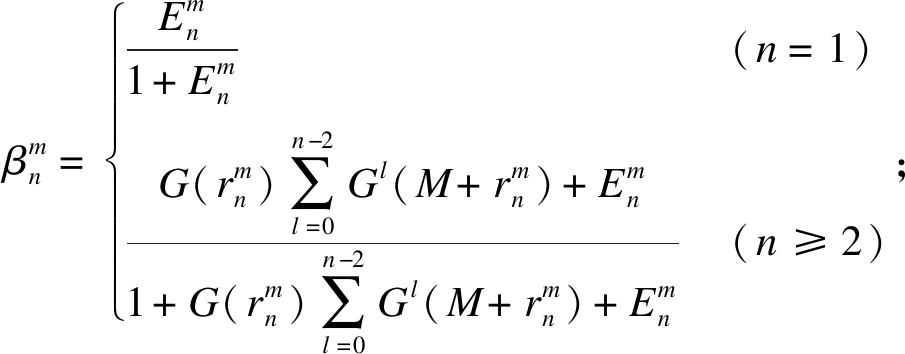
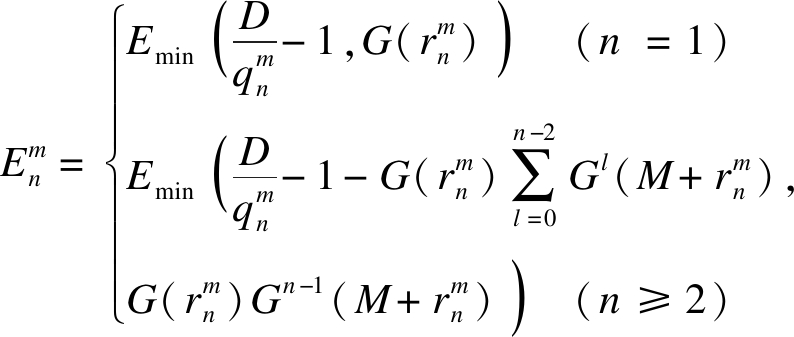
。
当公开产品曾售信息时,商家的预期收益为
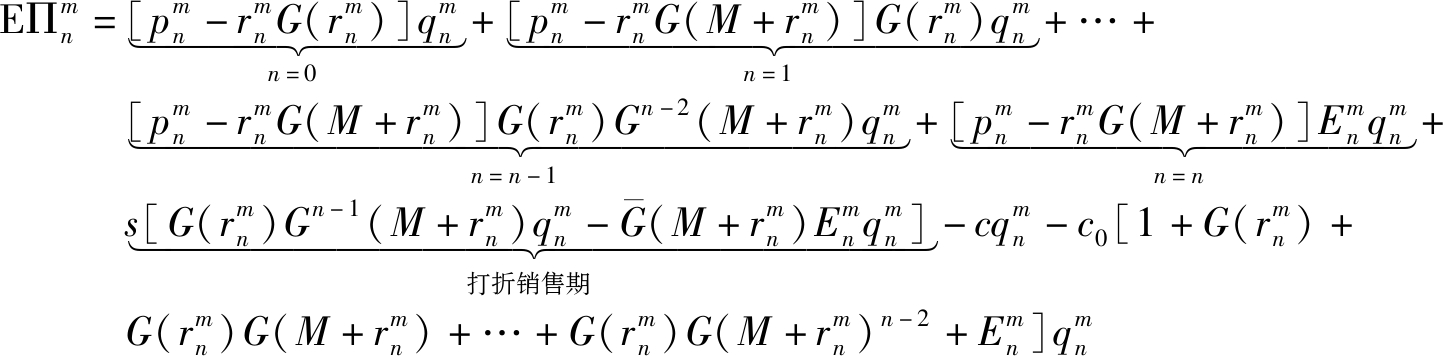
(5)
由式(4)、(5)可得
定理3 当向顾客公开产品曾售信息时,商家的最优决策为
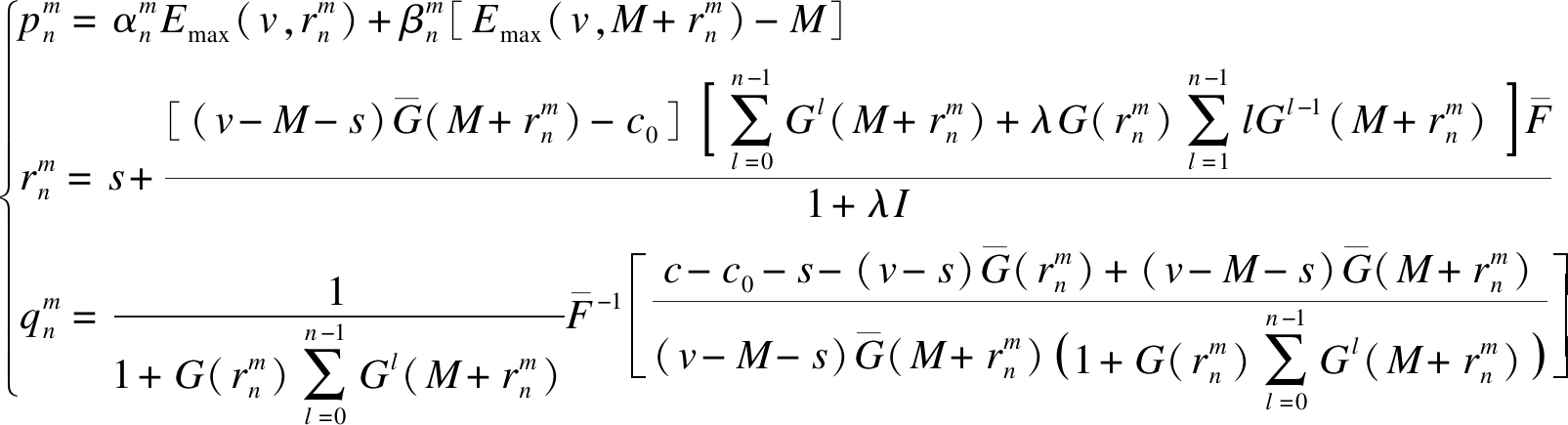
式中,
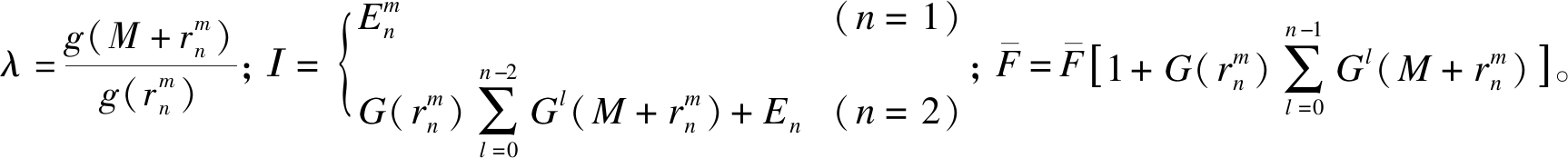
证明:由![]() 可得公开产品曾售信息时顾客的最大意愿,将式(4)代入可得
可得公开产品曾售信息时顾客的最大意愿,将式(4)代入可得![]() 整理可知
整理可知
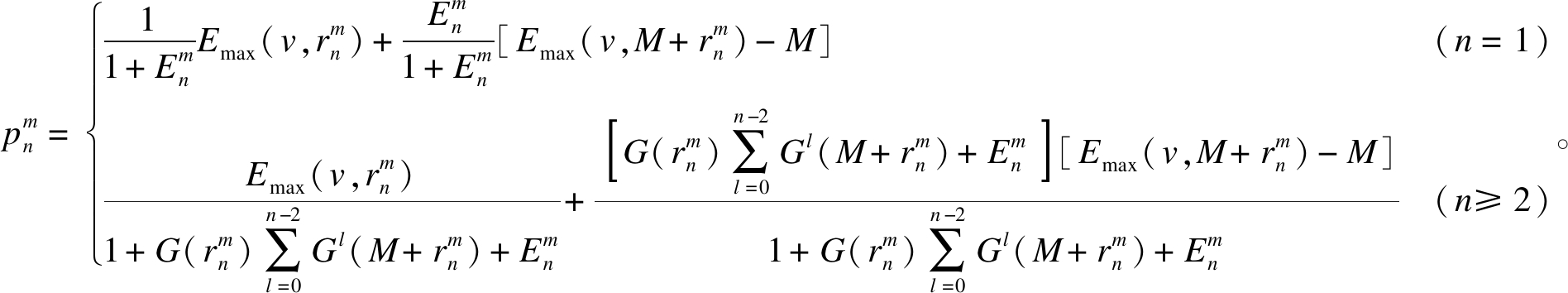
根据![]() 和
和![]() 可得商家最优的决策
可得商家最优的决策![]() 和
和![]() 将式(5)代入整理可得
将式(5)代入整理可得
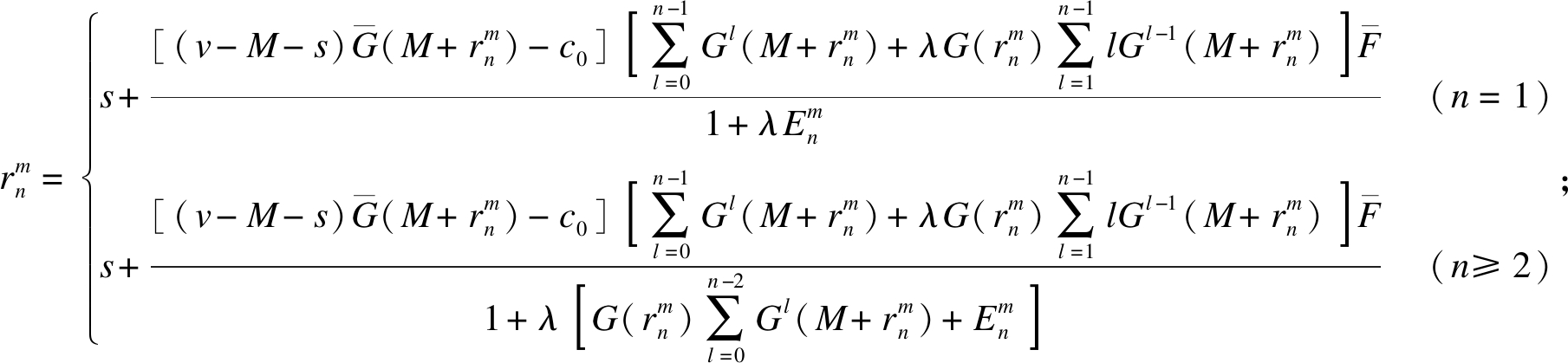
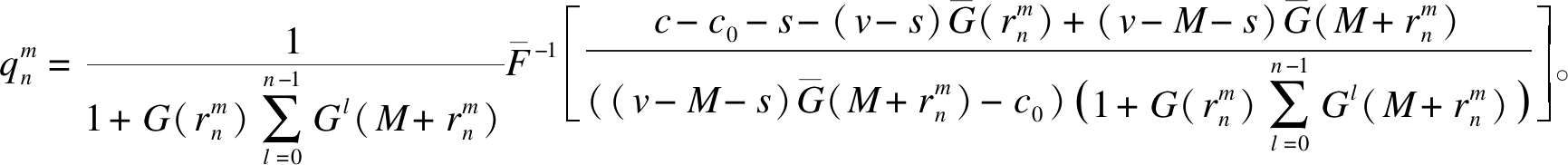 证毕。
证毕。
定理3给出了公开产品曾售信息时产品的最优销售价格、退货价格和库存。可以看出,产品最优退货价格是二次销售价值损害M的减函数,即公开产品曾售信息对产品在顾客心中价值的损害M越大,则退货价格![]() 越低。这说明公开产品曾售信息时,顾客越介意产品的曾售特征,则退货策略应越苛刻。在定理3中,
越低。这说明公开产品曾售信息时,顾客越介意产品的曾售特征,则退货策略应越苛刻。在定理3中,![]() 表示顾客购买全新产品的比例,
表示顾客购买全新产品的比例,![]() 表示顾客购买曾售产品的比例,
表示顾客购买曾售产品的比例,![]() 表示顾客购买单个全新产品可获得的价值,
表示顾客购买单个全新产品可获得的价值,![]() 表示顾客购买单个曾售产品可获得的价值。产品销售价格
表示顾客购买单个曾售产品可获得的价值。产品销售价格![]() 为顾客购买全新产品与曾售产品的价值期望,其中M对销售价格具有两方面作用:一方面,M增加,产品在顾客心中的价值降低,销售价格
为顾客购买全新产品与曾售产品的价值期望,其中M对销售价格具有两方面作用:一方面,M增加,产品在顾客心中的价值降低,销售价格![]() 降低,这是M对销售价格的负面影响;另一方面,M增加,顾客购买曾售产品的比例增加,销售价格
降低,这是M对销售价格的负面影响;另一方面,M增加,顾客购买曾售产品的比例增加,销售价格![]() 增加,这是M对销售价格的正面影响,且n越大这种正面影响越强。当公开产品曾售信息时,产品库存
增加,这是M对销售价格的正面影响,且n越大这种正面影响越强。当公开产品曾售信息时,产品库存![]() 是M的增函数,表明产品曾售对顾客效用损害越大则顾客退货率越低,二次销售对顾客剩余需求的满足作用越小,商家越需要通过增加进货量来满足顾客剩余需求。
是M的增函数,表明产品曾售对顾客效用损害越大则顾客退货率越低,二次销售对顾客剩余需求的满足作用越小,商家越需要通过增加进货量来满足顾客剩余需求。
五、算例分析
利用Matlab软件对上述模型进行算例分析。假设产品需求D和产品在顾客心中价值V均满足正态分布,D~N(2 000,50)和V~N(20,5);产品的生产成本c=14,再处理成本c0=2,清仓价格s=10;商家根据以往经验估计的供需比Γ和退货率Κ为常数,范围分别满足Γ∈[1,3]和Κ∈[0,1]。设计三组实验来验证销售价格p、退货价格r、真实库存q和收益EΠ的情况。
第一组实验,讨论隐藏产品曾售信息时,当供需比Γ和经验退货率Κ变化时,产品仅二次销售1次情形下(n=1)的销售价格p1、退货价格r1、真实库存q1和商家收益EΠ1的变化情况,结果如图4所示。
从图4中可以看出,隐藏产品曾售信息时销售价格p1和退货价格r1均随供需比Γ和经验退货率Κ的增加而降低,而真实库存q1和商家收益EΠ1随着供需比Γ和经验退货率Κ的增加而增加,且当供需比Γ较大时r1、q1、EΠ1的变化只与Κ相关,验证了定理1。
第二组实验,讨论隐藏产品曾售信息时,当供需比Γ和经验退货率Κ变化时,产品二次销售多次情形下(算例取n=2,3)销售价格pn、退货价格rn、真实库存qn和商家收益EΠn的变化情况,结果如图5所示。
图5清晰地表明,与仅二次销售1次时相同,产品销售价格pn和退货价格rn(n≥2)仍然是供需比Γ和经验退货率Κ的减函数,库存qn和收益EΠn是Γ和Κ的增函数。随着顾客退回产品二次销售次数n的增加,产品退货价格rn增加,但产品真实库存受到二次销售影响反而降低,验证了定理2。与库存相同,商家收益是二次销售次数n的减函数,说明二次销售次数的增加对商家收益具有一定负向作用。
第三组实验,讨论隐藏和公开产品曾售信息时,产品销售价格![]() 退货价格
退货价格![]() 和库存
和库存![]() 随产品曾售对其在顾客心中价值损害M的变化情况(算例取n=1,2,3),结果如图6所示。
随产品曾售对其在顾客心中价值损害M的变化情况(算例取n=1,2,3),结果如图6所示。
从图6中可以看出,公开曾售信息时产品退货价格低于隐藏产品曾售信息时![]() 产品退货价格
产品退货价格![]() 是价值损害M的减函数,即产品曾售对其在顾客心中价值损害越大,则产品退货价格越低。产品销售价格受M两方面影响:当n较小时(本例中n=1,2),产品销售价格主要受到M的负面影响,即
是价值损害M的减函数,即产品曾售对其在顾客心中价值损害越大,则产品退货价格越低。产品销售价格受M两方面影响:当n较小时(本例中n=1,2),产品销售价格主要受到M的负面影响,即![]() 随着M的增加而降低;当n较大时(本例中n=3),产品销售价格主要受到M的正面影响,即
随着M的增加而降低;当n较大时(本例中n=3),产品销售价格主要受到M的正面影响,即![]() 随着M的增加而提高。这验证了定理3的结论。产品库存
随着M的增加而提高。这验证了定理3的结论。产品库存![]() 是M的增函数,即产品曾售对其在顾客心中价值损害越大,则商家公开产品曾售信息时的进货量越大。
是M的增函数,即产品曾售对其在顾客心中价值损害越大,则商家公开产品曾售信息时的进货量越大。
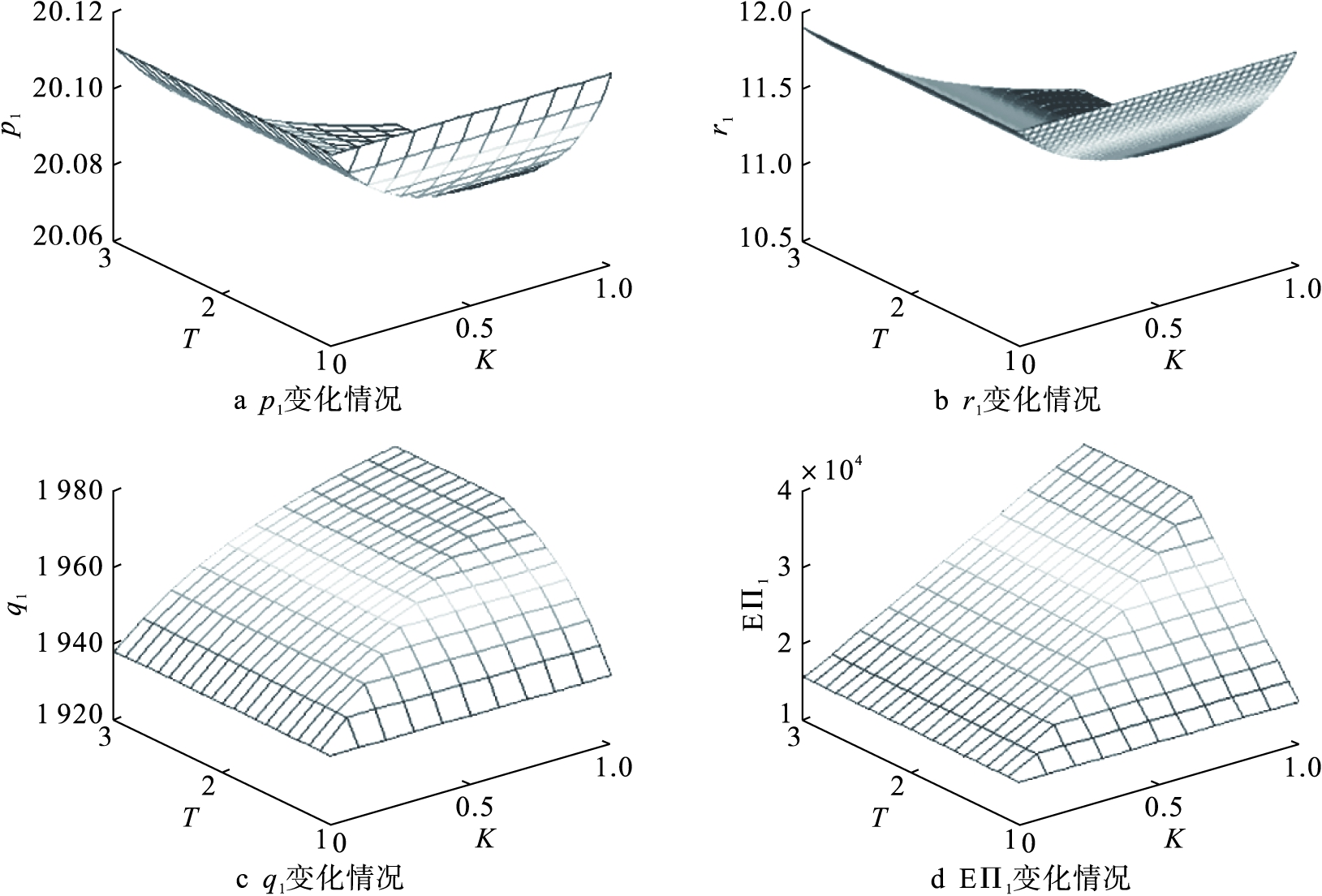
图4 产品二次销售1次时p1,r1,q1,EΠ1变化情况
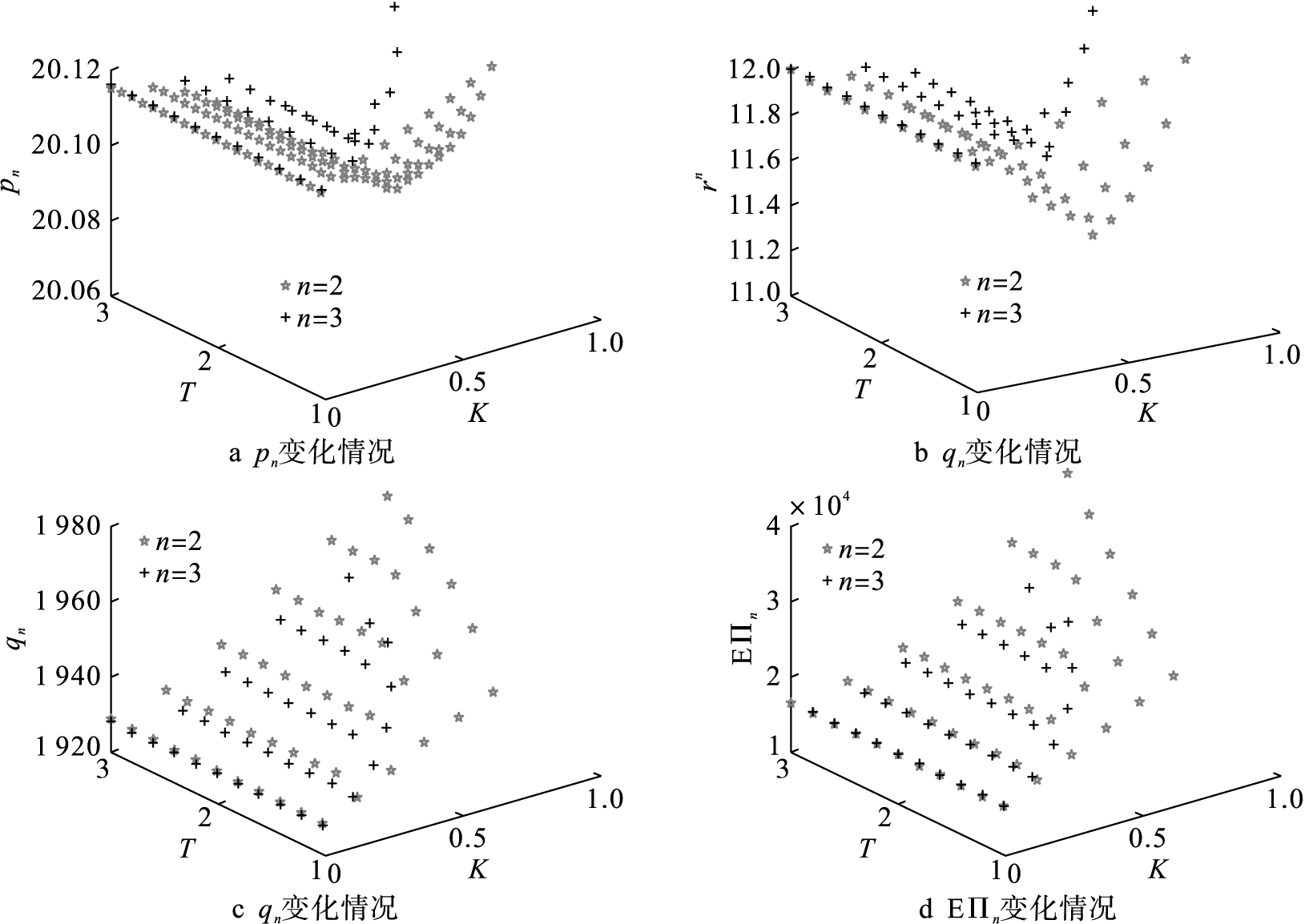
图5 产品二次销售n次时pn,rn,qn,EΠn变化情况
六、总 结
本文基于顾客战略行为,在假设售出产品会发生退货并二次销售的条件下,分别研究隐藏和公开产品曾售信息两类情形下的商家最优无理由退货策略问题,得出了最优产品退货价格、销售价格和库存策略。
通过对上述决策变量进行分析可知:当隐藏产品曾售信息时,产品退货价格是再销售成本的减函数;当再销售总成本高于打折价格时,其高于不允许二次销售的情形,且是产品二次销售次数的增函数;与不允许二次销售时相同,产品销售价格仍是顾客对产品感知价值和退货价格最大值的期望,二次销售次数越多则销售价格越高;产品库存是二次销售次数的减函数,这是由于二次销售增加了同一产品的销售次数。当公开产品曾售信息时,顾客对产品的感知价值会受到损害,设价值损害为常数,则产品退货价格是其减函数;产品销售价格受到该价值损害正、负两方面的综合作用,且二次销售次数越多则价值损害对价格的正面作用越明显;产品库存是价值损害的增函数,说明价值损害越大则商家公开产品曾售信息时所需库存量越大。
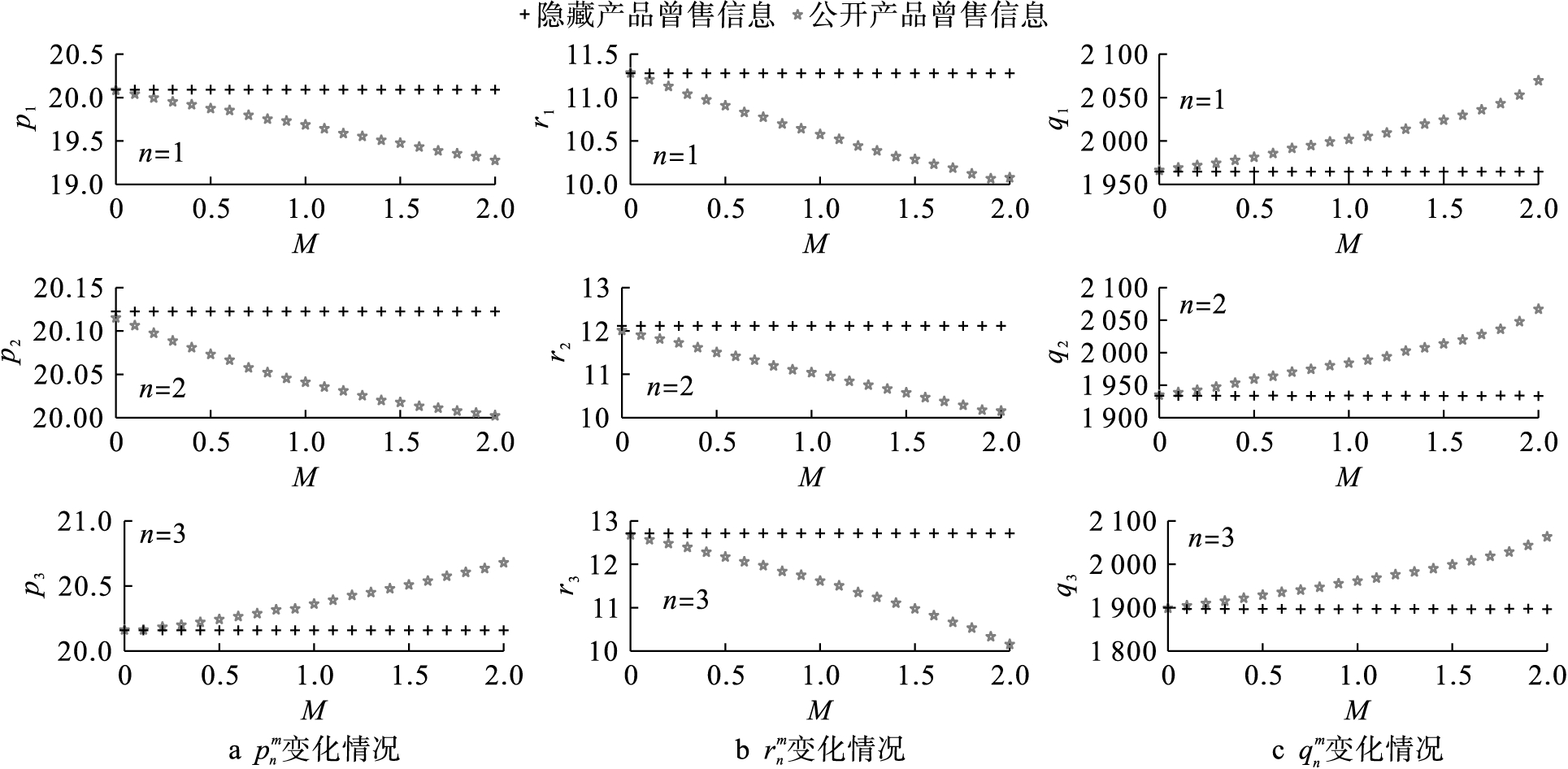
图6 隐藏和公开产品曾售信息时![]() 随M变化情况
随M变化情况
[1] 李淑梅,金亮.消费者理性预期下的线上零售商定价与退款保证策略研究 [J].软科学,2018,32(12):115-120.
[2] Davis S,Gerstner E,Hagerty M.Money back guarantees in retailing:matching products to consumer tastes [J].Journal of Retailing,1995,71(1):7-22.
[3] Akçay Y,Boyac T,Zhang D.Selling with money-back guarantees:the impact on prices,quantities,and retail profitability [J].Production and Operations Management,2013,22(4):777-791.
T,Zhang D.Selling with money-back guarantees:the impact on prices,quantities,and retail profitability [J].Production and Operations Management,2013,22(4):777-791.
[4] 熊中楷,李豪,彭志强.竞争环境下季节性产品网上直销动态定价模型 [J].系统工程理论与实践,2010,30(2):243-250.
[5] 毛可,傅科,徐佳焱.无理由退货政策下的概率销售策略 [J].系统工程理论与实践,2020,40(4):964-977.
[6] 何啸源,甄学平,刘斌.考虑双退货期限的在线零售商退货策略研究 [J].上海管理科学,2018,40(4):85-88.
[7] McWilliams B.Money-back guarantees:helping the low-quality retailer [J].Management Science,2012,58(8):1521-1524.
[8] Hess J D,Chu W J,Gerstner E.Controlling product returns in direct marketing [J].Marketing Letters,1996,7(4):307-317.
[9] Chu W J,Gerstner E,Hess J D.Managing dissatisfaction [J].Journal of Service Research,1998,1(2):140-155.
[10] Su X M.Consumer returns policies and supply chain performance [J].Manufacturing & Service Operations Management,2009,11(4):595-612.
[11] Hsiao L,Chen Y J.Return policy:hassle-free or your money-back guarantee? [J].Naval Research Logistics,2014,61(5):403-417.
[12] 孙军,孙亮.基于无缺陷退货的在线零售商运费承担策略研究 [J].软科学,2014,28(6):41-45.
[13] 郑春东,刘一凡,邹孟.退货运费险对网购消费者购买意愿的影响 [J].沈阳工业大学学报(社会科学版),2016,9(2):150-156.
[14] Giri B C,Roy B,Maiti T.Multi-manufacturer pricing and quality management strategies in the presence of brand differentiation and return policy [J].Computers & Industrial Engineering,2017,105(3):146-157.
[15] 李建斌,李赟.无理由退货政策下的在线定价及补偿优化策略 [J].系统工程理论与实践,2016,36(11):2811-2819.
[16] 曾诚,邵晓峰.互联网环境下客户定制化产品的定价及分段退货策略研究 [J].上海管理科学,2019,41(5):31-36.
[17] 杨道箭,张秀杰.不确定需求下全渠道运营退货策略 [J].预测,2020,39(2):84-89.
[18] 吴红迪,李新剑.权力失衡下的退货策略优化研究 [J].怀化学院学报,2019,38(2):47-50.
[19] 周振红,黄深泽.随机需求下考虑顾客策略行为的预售和退货策略 [J].系统管理学报,2019,28(2):277-284.
[20] Su X M,Zhang F Q.Strategic customer behavior,commitment,and supply chain performance [J].Mana-gement Science,2008,54(10):1759-1773.